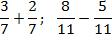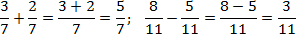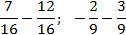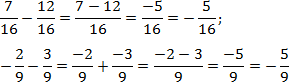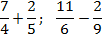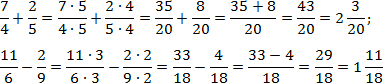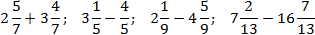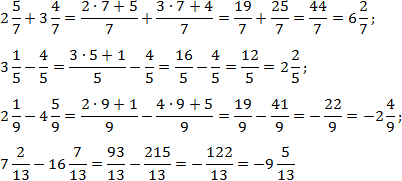Как решать дроби минусовать
Вычитание дробей
4 класс, 5 класс, 6 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Есть два формата записи:
Над чертой принято писать делимое, которое является числителем. А под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дробей
1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Равными называют a/b и c/d в том случае, если a * d = b * c.
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Правило вычитания дробей
Вычитание — арифметическое действие, когда от одного числа отнимают другое.
Свойства вычитания:
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Вычитание дробей с одинаковыми знаменателями
Для вычитания дробей с одинаковыми знаменателями нужно от числителя первой отнять числитель второй, а знаменатель оставить тот же.
Прежде, чем зафиксировать ответ, важно проверить возможность сокращения.
Рассмотрим это правило на примере:
Вычитание дробей с разными знаменателями
Как вычитать дроби с разными знаменателями? Для этого приводим их к общему знаменателю и гаходим разность числителей.
Рассмотрим пример, в котором нужно найти разность 2/9 и 1/15.
Как решаем:
НОК (9, 15) = 3 * 3 * 5 = 45
Вычитание обыкновенной дроби из натурального числа
Для вычитания из обыкновенной дроби натурального числа необходимо это действие привести к вычитанию обыкновенных дробей.
Разберем для наглядности пример разности 3 и 6/7.
Как решаем:
Ответ: две целых одна седьмая.
Вычитание натурального числа из обыкновенной дроби
Для вычитания натурального числа из обыкновенной дроби нужно последовать тому же алгоритму, что и в предыдущем примере. А именно: перевести натуральное число в вид дроби, привести все к единому знаменателю, найти разность.
Рассмотрим пример разности 3 из 83/21.
Как решаем:
А еще можно вот так:
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.
Вычитание дробей
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями записывают так:
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби, знаменатель которой равен знаменателю вычитаемой дроби.

| 7 |
| 7 |
и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого (что вычитаем).
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно привести к общему знаменателю дробные части, а затем выполнить вычитание целой части из целой, а дробной из дробной.
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Так как у дробных частей разные знаменатели, то как и во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
Сложим полученную неправильную дробь
| 18 |
| 18 |
и дробную часть уменьшаемого и получим:
Все рассмотренные случаи можно описать с помощью правил вычитания смешанных чисел.
Вычитание обыкновенных дробей: правила, примеры, решения
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Решение
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Решение
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Решение
Подсчитаем: 2 9 = 2 · 5 9 · 5 = 10 45 1 15 = 1 · 3 15 · 3 = 3 45
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Решение
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Решение
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Решение
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Решение
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Решение
Краткая запись всего решения:
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Решение
Дроби. Вычитание дробей.
Вычитание дробей с одинаковыми знаменателями.
Для нахождения разницы 2х дробей с одинаковыми знаменателями, необходимо вычесть из числителя 1й дроби числитель 2й дроби, а знаменатель обоих дробей оставить не изменяя. Вычитание обыкновенных дробей:
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь, которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:


Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной, единицу переводят к виду неправильной дроби, у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7, т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей – правильной из целого числа (натурального числа) :
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей.
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ), и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители, то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Сложение и вычитание дробей
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.