Как решать дроби крестом
Решение уравнений с пропорцией
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Произведение крайних членов пропорции равно произведению средних.
Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Если в члене пропорции присутствуют знаки « + » или « − », обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.
После заключения в скобки члена пропорции « (2 − x) » используем правило пропорции для дальнейшего решения.
Теперь раскроем скобки с помощью правила раскрытия скобок.
Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение, в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления « : » можно заменить на дробную черту.
Методы решения уравнений, содержащих дроби
В этой статье я расскажу методики решения рациональных уравнений, содержащих дроби.
В свою очередь рациональные уравнения делятся на два вида: целые рациональные и дробные рациональные.
К целым рациональным уравнениям относятся линейные и квадратные уравнения. Рассмотрим пример:
Это уравнение является. попробуешь угадать?. линейным. Его можно запросто увидеть, если деление на 2 и на 6 заменить умножением на 1/2 и 1/6 соответственно. Но оно все-таки содержит в себе знаменатель, поэтому мы его и рассматриваем в данной статье.
К дробным рациональным уравнениям относятся уравнения, которые содержат икс в знаменателе. Например, это уравнение дробное рациональное:
Методика решения приведенных примеров, в принципе, одинакова. Разница состоит в том, что в дробных рациональных уравнениях знаменатель не должен равняться нулю, поэтому при их решении оговаривают ограничения для икса. По-научному говорят, что находят область допустимых значений (ОДЗ).
Но давайте начнем с простого.
Целое рациональное уравнение.
Сначала решим целое рациональное уравнение.
Если ты в уравнении видишь дроби, то надо от них избавится, ведь уравнение без дробей решается намного приятнее)
В этом уравнении находим общий знаменатель. Он равен 6. Это значит, что обе части уравнения надо умножить на 6 (одинокий икс тоже).
Обычно этот шаг пропускают и переходят к следующему, но я его все равно распишу:
Числители и знаменатели сокращаются и получается элементарное уравнение:
Приводим подобные слагаемые:
Дробное рациональное уравнение.
Теперь решим дробное рациональное уравнение.
Я уже писала о том, что в дробных рациональных уравнениях знаменатели не должны равняться нулю. Знаменатель второй дроби нас устраивает, ведь 3 не равно 0) А вот знаменатель первой дроби требует от нас, чтобы мы нашли ОДЗ.
А дальше по накатанной: надо обе части уравнения умножить на общий знаменатель. Общим знаменателем будет выражение 3(х + 9).
Снова распишу подробно, но если ты шаришь, то следующую запись можешь не писать.
Сравниваем с ОДЗ. Всё отлично. Корень уравнения подходит.
Альтернативный метод решения уравнения с дробями.
Но нельзя пройти мимо другого метода решения данного уравнения: с помощью пропорции. Помнишь, как она раскрывается? Правильно, крест-накрест. И не надо искать общий знаменатель)
Перемножаем. и о чудо! Получаем уравнение, которое мы уже решали!
Дальнейшее решение расписывать не буду, оно есть выше.
Такой способ решения уравнений хорош, когда в уравнении имеются две дроби.
В завершении решу еще одно уравнение предложенными выше способами.
Только ты решаешь какой способ выбрать.
Твой персональный препод Васильева Анна)
Решение уравнений с дробями
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Понятие дробного уравненияДробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так: Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе. Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры: На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное. Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение. Как решать уравнения с дробями1. Метод пропорцииЧтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает. Итак, у нас есть линейное уравнение с дробями: В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь. После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели. 2. Метод избавления от дробейВозьмем то же самое уравнение, но попробуем решить его по-другому. В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать: Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля! Вот так просто мы получили тот же ответ, что и в прошлый раз. Что еще важно учитывать при решенииУниверсальный алгоритм решенияОпределить область допустимых значений. Найти общий знаменатель. Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут. Раскрыть скобки, если нужно и привести подобные слагаемые. Решить полученное уравнение. Сравнить полученные корни с областью допустимых значений. Записать ответ, который прошел проверку. Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах. Примеры решения дробных уравненийЧтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек. Пример 1. Решить дробное уравнение: 1/x + 2 = 5. Пример 2. Найти корень уравнения Пример 3. Решить дробное уравнение: Если x = 3 — знаменатель тоже равен нулю. Рациональные уравнения с примерами решенияСодержание: Рациональные уравнения. Равносильные уравнениядва уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют. Так, например, равносильными будут уравнения Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения. 1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному; 2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному; 3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному. Левая и правая части каждого из них являются рациональными выражениями. Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями. Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе. Применение условия равенства дроби нулюНапомним, что Пример №202Решите уравнение Решение: С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду Окончательно получим уравнение: Чтобы дробь Тогда Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так: Значит, решая дробное рациональное уравнение, можно: 1) с помощью тождественных преобразований привести уравнение к виду 2) приравнять числитель 3) исключить из его корней те, при которых знаменатель Использование основного свойства пропорцииЕсли Пример №203Решите уравнение Решение: Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Сложив выражения в правой части уравнения, приведем его к виду: По основному свойству пропорции имеем: Решим это уравнение: Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем. Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так: Таким образом, для решения дробного рационального уравнения можно: 1) найти область допустимых значений (ОДЗ) переменной в уравнении; 2) привести уравнение к виду 3) записать целое уравнение 4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ. Метод умножения обеих частей уравнения на общий знаменатель дробейПример №204Решите уравнение Решение: Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители: Областью допустимых значений переменной будут те значения Умножим обе части уравнения на это выражение: Получим: Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем. Решая дробное рациональное уравнение, можно: 3) умножить обе части уравнения на этот общий знаменатель; 4) решить полученное целое уравнение; 5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ. Пример №205Являются ли равносильными уравнения Решение: Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений. Степень с целым показателемНапомним, что в 7 классе мы изучали степень с натуральным показателем. По определению: где В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: Рассмотрим степени числа 3 с показателями В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим: Число Нулевая степень отличного от нуля числа а равна единице, то есть Вернемся к строке со степенями числа 3, где слева от числа Приходим к следующему определению степени с целым отрицательным показателем: если
|
|---|









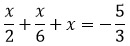
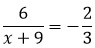
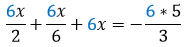
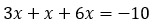
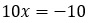
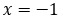
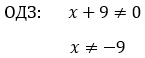
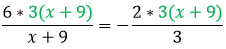
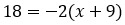
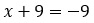
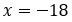

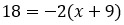















 когда
когда 

 где
где  и
и  — целые рациональные выражения. Имеем:
— целые рациональные выражения. Имеем:

 равнялась нулю, нужно, чтобы числитель
равнялась нулю, нужно, чтобы числитель  равнялся нулю, а знаменатель
равнялся нулю, а знаменатель  не равнялся нулю.
не равнялся нулю. откуда
откуда  При
При  знаменатель
знаменатель  Следовательно,
Следовательно,  — единственный корень уравнения.
— единственный корень уравнения.

 к нулю и решить полученное целое уравнение;
к нулю и решить полученное целое уравнение; равен нулю, и записать ответ.
равен нулю, и записать ответ. то
то  где
где 

 Имеем:
Имеем:  то есть ОДЗ переменной
то есть ОДЗ переменной  содержит все числа, кроме 1 и 2.
содержит все числа, кроме 1 и 2. получив пропорцию:
получив пропорцию: 

 откуда
откуда 


 и решить его;
и решить его;

 при которых
при которых  то есть все значения
то есть все значения  кроме чисел
кроме чисел  А простейшим общим знаменателем будет выражение
А простейшим общим знаменателем будет выражение 

 а после упрощения:
а после упрощения:  то есть
то есть  откуда
откуда  или
или 


 — натуральное число,
— натуральное число, 
 кг. Как понимать смысл записи
кг. Как понимать смысл записи 
 — это соответственно
— это соответственно 

 должно быть втрое меньше числа
должно быть втрое меньше числа  равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно,
равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно,  Равенство
Равенство  справедливо для любого основания
справедливо для любого основания  при условии, что
при условии, что 
 при
при 
 записано число
записано число  Это число втрое меньше, чем 1, то есть равно
Это число втрое меньше, чем 1, то есть равно  Следовательно,
Следовательно,  Рассуждая аналогично получаем:
Рассуждая аналогично получаем:  и т. д.
и т. д. натуральное число, то
натуральное число, то 