Как решать делимость чисел
Признаки делимости чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Что такое «признак делимости»
Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.
Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.
Однозначные, двузначные и трехзначные числа
Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.
Трехзначные числа — числа, в составе которых три знака (три цифры).
Чётные и нечётные числа
Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!
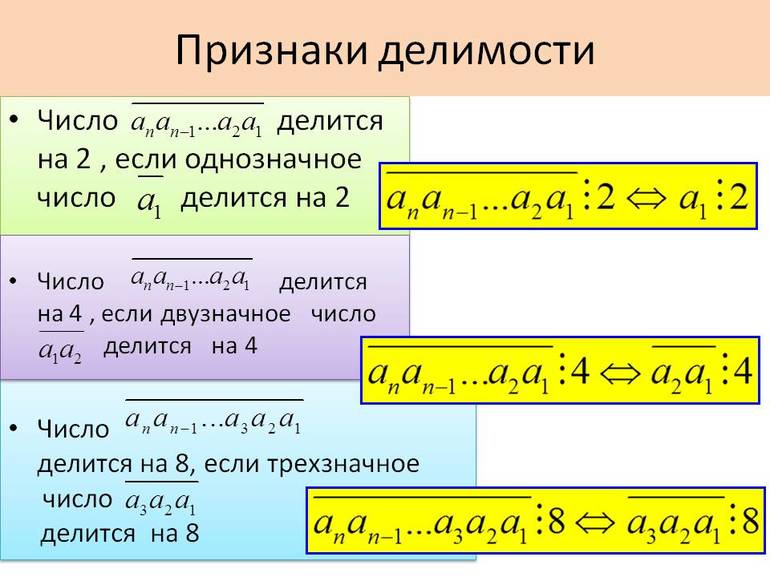
Признаки делимости чисел
Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.
Признак делимости на 3. Сумма цифр числа должна делиться на 3.
Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.
Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.
Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.
Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.
Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.
Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.
Признаки делимости чисел
В данной публикации мы рассмотрим признаки делимости на числа от 2 до 11, сопроводив их примерами для лучшего понимания.
Признак делимости – это алгоритм, используя который можно сравнительно быстро определить, является ли рассматриваемое число кратным заранее заданному (т.е. делится ли на него без остатка).
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра является четной, т.е. также делится на два.
Примеры:
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма всех его цифр, также, делится на три.
Примеры:
Признак делимости на 4
Двузначное число
Число делится на 4 тогда и только тогда, когда сумма удвоенной цифры в разряде его десятков и цифры в разряде единиц, также, делится на четыре.
Число разрядов больше 2
Число кратно 4, когда две его последние цифры образуют число, делящееся на четыре.
Примечание:
Число делится на 4 без остатка, если:
Признак делимости на 5
Число делится на 5 тогда и только тогда, когда его последняя цифра – это 0 или 5.
Примеры:
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда он одновременно кратно и двум, и трем (см. признаки выше).
Примеры:
Признак делимости на 7
Число делится на 7 тогда и только тогда, когда сумма утроенного числа его десятков и цифры в разряде единиц, также, делится на семь.
Признак делимости на 8
Трехзначное число
Число делится на 8 тогда и только тогда, когда сумма цифры в разряде единиц, удвоенной цифры в разряде десятков и учетверенной в разряде сотен делится на восемь.
Число разрядов больше 3
Число делится на 8, когда три последние цифры образуют число, делящееся на 8.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма всех его цифр, также, делится на девять.
Примеры:
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.
Примеры:
Признак делимости на 11
Число делится на 11 тогда и только тогда, когда модуль разности сумм четных и нечетных разрядов равен нулю или делится на одиннадцать.
Примеры:
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.
Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Свойства делителей от 6 до 10
Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.
Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.
Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:
Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.
В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:
Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.
Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Разрядные единицы
Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:
Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.
Делители от 11 и выше
Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Онлайн-задание с ответом: 7535, 74019 и 50486.
Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:
Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:
В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:
Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.
Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.
Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.
Например, 6942:
Еще пример — 754:
Признак делимости на составное число
Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.
Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.
Таблица кратных от 2 до 10
Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:
| Делимость на: | Признак числа: |
| 2 | Оканчивается четной цифрой: 0, 2, 4,6, 8 |
| 3 | Сумма цифр, их которой оно состоит, делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Окончание на 5 или 0 |
| 6 | Одновременная кратность 2 и 3 |
| 8 | Три последние цифры кратны 8 |
| 9 | Сумма цифр кратна 3 |
| 10 | Окончание равно нулю |
Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
Делимость чисел. Признаки делимости
Делитель числа
Пусть a и b – целые числа.
В этом случае говорят, что a делится на b нацело или a кратно b.
Также говорят о делимости a на b.
Например, множество всех целых делителей числа 12:
Если число a имеет два взаимно простых делителя b и c, то произведение bc также является делителем для a:
Число 105 делится на 3 и на 5. Значит, оно также делится на 15, т.е. 105 ⋮ 15
Число 231 делится на 7 и на 11. Значит, оно также делится на 77, т.е. 231 ⋮ 77
Признаки делимости
Чтобы определить делимость без самого деления, существует набор методов «экспресс-анализа», которые называют признаками делимости.
Двузначные грани числа – разбиение числа на группы по 2 цифры, считая справа налево. Например: 1|23|45|67.
Трёхзначные грани числа – разбиение числа на группы по 3 цифры, считая справа налево. Например: 1|234|567.
Знакопеременная сумма граней – каждая грань входит со знаком +/-, последняя с +.
Число заканчивается чётной цифрой
Сумма цифр числа делится на 3
Число, составленное из двух последних цифр, делится на 4
Число заканчивается на 0 или 5
Число, полученное вычитанием удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 7
Знакопеременная сумма 3-значных граней числа делится на 7
Число, составленное из трёх последних цифр, делится на 8
Сумма цифр числа делится на 9
Число заканчивается на 0
Сумма цифр на нечётных позициях и сумма цифр на нечётных позициях либо равны, либо отличаются на число, кратное 11
Знакопеременная сумма цифр делится на 11 или равна 0
Число, полученное добавлением учетверенной последней цифры к исходному числу с отброшенной последней цифрой, делится на 13
Знакопеременная сумма 3-значных граней числа делится на 13
Число, полученное добавлением последней цифры, умноженной на 12, к исходному числу с отброшенной последней цифрой, делится на 17
Число, полученное вычитанием последней цифры, умноженной на 5, к исходному числу с отброшенной последней цифрой, делится на 17
Число, полученное добавлением удвоенной последней цифры из исходного числа с отброшенной последней цифрой, делится на 19
Число, полученное добавлением утроенного числа из двух последних цифр с числом сотен, делится на 23.
n последних цифр числа – нули
Примеры
Пример 1. Число 15464*543 делится на 3. Какие цифры могут стоять на месте звёздочки?
Обозначим цифру на месте звёздочки x. Сумма всех цифр:
Сумма должна делиться на 3:
Пример 2. Число 14*6* делится на 45. Какое это число?
Делимость на 9 требует сумму цифр, кратную 9: 1+4+x+6+y = 9k
Делимость на 5 даёт y = 0 или y = 5.
Получаем, учитывая, что x,y – цифры:
Ответ: 14760 или 14265
Пример 3. В течение месяца три воскресенья пришлись на чётные числа. Какие это числа? Каким днём недели было 7 число этого месяца?
Из последнего неравенства получаем, что a = 2.
Значит, воскресенья были 2, 16 и 30 числа.
Получаем, что 7 число было в пятницу.
Ответ: 2,16 и 30 числа; пятница.
Пример 4. Является ли число 12345678926 квадратом?
Две последние цифры данного числа дают 26, при делении на 4 получаем:
Таким образом, данное число не делится на 4 и не может быть квадратом.
Сумма цифр данного числа 1+8 = 9 – делится на 9.
Делимость чисел. Признаки делимости. Основная теорема арифметики
В этой статье – необходимая теория для решения задачи 18 Профильного ЕГЭ по математике. Но это не все. Знания о числах и их свойствах, признаки делимости и формула деления с остатком могут пригодиться вам при решении многих задач ЕГЭ.
Повторим еще раз, какие бывают числа.
Например, при делении 9 на 4 мы получаем частное 2 и остаток 1, то есть 9 = 4∙2 + 1.
Простые числа – те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19…
Числа называются взаимно простыми, если они не имеют общих делителей, кроме 1.
Любое натуральное число можно разложить на простые множители.
Например, 72 = 2∙2∙2∙3∙3, а 98 = 2∙7∙7.
Основная теорема арифметики: Любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.
Наименьшее общее кратное двух чисел (НОК) — это наименьшее число, которое делится на оба данных числа.
Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое делятся два данных числа.
последняя цифра числа четная;
сумма цифр числа делится на 3;
число заканчивается на 0 или на 5;
сумма цифр числа делится на 9;
последняя цифра числа равна 0;
суммы цифр на четных и нечетных позициях числа равны или их разность кратна 11.