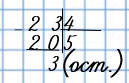Как решать деление с остатком
Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как сделать проверку?
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
Порядок решения
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
Поделись с друзьями в социальных сетях:
Деление с остатком
Не всегда можно полностью разделить одно число на другое. В примерах на деление может оставаться остаток. Такое деление называется деление с остатком.
Деление с остатком — это деление одного натурального числа на другое, при котором остаток не равен нулю.
Если при делении натуральных чисел остаток равен нулю, то говорят, что делимое делится на делитель без остатка, или, иначе говоря, делится нацело.
Деление с остатком записывают так:
Читается пример следующим образом:
« 17 » разделить на « 3 » получится « 5 » и остаток « 2 ».
Порядок решения примеров на деление с остатком.
При делении с остатком остаток всегда должен быть меньше делителя.
Если получилось, что остаток больше делителя, значит, вы неверно нашли наибольшее число, которое делится на делитель без остатка.
При решении более сложных примеров не всегда можно легко найти наибольшее число из пункта 1. Иногда для этого необходимо произвести дополнительные расчёты в столбик. Покажем это на примере.
Методом подбора найдём на сколько надо умножить « 27 », чтобы получить ближайшее число к « 190 ».
Попробуем умножить на « 6 ».
Рассчитаем остаток и сравним его с делителем.
Остаток больше делителя. Это означает, что « 6 » как множитель нам не подходит. Попробуем умножить делитель на « 7 ».
Снова рассчитаем и сравним остаток с делителем.
Остаток меньше делителя. Значит пример решён верно. Запишем ответ.
Все вычисления выше можно представить в виде деления в столбик. Правила деления в столбик вы можете освежить в уроке «Деление в столбик» на нашем сайте.
Как проверить деление с остатком
Проверим ответ нашего примера.
Деление с остатком выполнено верно.
Если при делении с остатком делимое меньше делителя, то их неполное частное равно нулю, остаток равен делимому.
Другими словами, если вы делите меньшее число на большее, неполное частное всегда будет равно нулю.
Деление с остатком. Формула деления с остатком и проверка.
Деление с остатком.
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.
Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?
Решение:
Поделим число 16 на 5 столбиком получим:

Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.
a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.
Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.
Остаток от деления
Остаток всегда должен быть меньше делителя.
Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.
Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.
Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.
Остаток может быть равен делителю?
Ответ: нет.
Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)
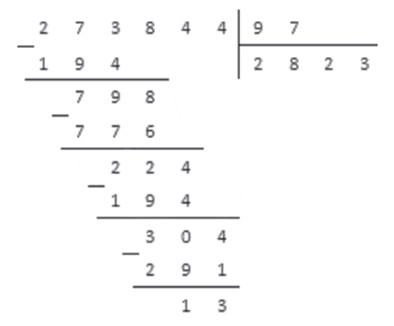
Пример №1:
Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8
Решение:
а) Делим столбиком:
258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6 Category: 5 класс, Натуральные числа Leave a comment
Деление натуральных чисел с остатком: правило, примеры решений
Многие числа нельзя разделить нацело, при делении часто присутствует остаток, отличный от нуля. В этой статье мы разберем способы деления натуральных чисел с остатком и подробно рассмотрим их применение на примерах.
Начнем с деления натуральных чисел с остатком в столбик, затем рассмотрим деление с помощью последовательного вычитания. Наконец, закончим разбором метода подбора неполного частного. Приведем алгоритм деления с остатком для наиболее общего случая и покажем, как проводить проверку результата деления натуральных чисел с остатком.
Деление натуральных чисел столбиком с остатком
Это один из самых удобных способов деления. Подробно он описан в отдельной статье, посвященной делению натуральных чисел столбиком. Здесь мы не будем приводить всю теорию заново, но сконцентрируемся именно на случае деления с остатком.
Приведем решение примера, так как понять суть метода проще всего на практике.
Пример 1. Как делить натуральные числа с остатком?
Проводим деление столбиком и записываем:
Деление чисел с остатком через последовательное вычитание
Чтобы найти неполное частное и остаток, можно прибегнуть к последовательному вычитанию делителя из делимого. Этот способ не всегда целесообразен, однако в некоторых случаях его очень удобно применять. Вновь обратимся к примеру.
Пример 2. Деление с остатком через последовательное вычитание.
Рассмотрим еще один пример. На этот раз, приведем только математические выкладки, не прибегая к аналогиям.
Пример 3. Деление с остатком через последовательное вычитание.
Повторяем эту операцию еще раз:
Метод последовательного вычитания непригоден, когда делимое меньше делителя. В таком случае можно сразу записать ответ: неполное частное равно нулю, а остаток равен самому делимому.
12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)
Также касательно метода последовательного вычитания нужно отметить, что он удобен только в случаях, когда вся операция деления сводится к небольшому количеству вычитаний. Если делимое во много раз больше делителя, использование этого метода будет нецелесообразно и связано с множеством громоздких вычислений.
Метод подбора неполного частного
При делении натуральных чисел с остатком можно вычислить результат методом подбора неполного частного. Покажем, как можно вести процесс подбора, и на чем он основан.
В-третьих, не будем забывать, что остаток всегда меньше делителя.
Разберем применение этого метода на примере.
Пример 4. Деление с остатком методом подбора
Алгоритм деления натуральных чисел с остатком
Когда рассмотренные выше методы подбора неполного частного и последовательного вычитания требуют слишком громоздких вычислений, для деления с остатком применяется следующий метод. Рассмотрим алгоритм деления натурального числа a на число b с остатком.
Сформулируем три вопроса и ответим на них:
Запомним это число.
2. Справа в записи делителя допишем число нулей, определенное разницей между количеством знаков в делимом и делителе. В нашем случае нужно дописать один нуль. Если записанное число больше делимого, то нужно из запомненного в первом пункте числа вычесть единицу.
Число, которое мы получили на предпоследнем шаге ( 470 = 47 · 10 ) является первым из искомых слагаемых.
5. Найдем разность между делимым и первым найденным слагаемым. Если полученное число больше делителя, то переходим к нахождению второго слагаемого.
3. Так как в предыдущем пункте мы получили число 0 и запомнили его, нам не нужно прибавлять ни одного нуля к единице справа. Таким образом, рабочим разрядом являются единицы
899 = 47 · 10 + 47 · 9 + 6
Применим распределительное свойство умножения.
899 = 47 · 10 + 47 · 9 + 6 = 47 · ( 10 + 9 ) + 6
Безусловно, при решении практических примеров нет нужды расписывать все действия так подробно. Покажем это:
Пример 5. Деление натуральных чисел с остатком
В результате получаем:
42252 = 40800 + 1360 + 68 + 24 = 68 · 600 + 68 · 20 + 68 · 1 + 24 = = 68 · ( 600 + 20 + 1 ) + 24 = 68 · 621 + 24
Деление натуральных чисел с остатком. Проверка результата
Деление натуральных чисел с остатком, особенно при больших числах, довольно трудоемкий и громоздкий процесс. Допустить ошибку в вычислениях может каждый. Именно поэтому, проверка результата деления поможет понять, все ли вы сделали правильно. Проверка результата деления натуральных чисел с остатком выполняется в два этапа.
На первом этапе проверяем, не получился ли остаток больше делителя. Если нет, то все хорошо. Иначе, можно сделать вывод, что что-то пошло не так.
Остаток всегда меньше делителя!
Пример 6. Проверка результата деления натуральных чисел с остатком.
Значит, деление выполнено неверно.
Первый пункт проверки пройден, переходим ко второму.
Подставляем значения и сравниваем результаты
13 · 9 + 5 = 117 + 5 = 122 ; 121 ≠ 122
Значит, в вычисления школьника где-то закралась ошибка.
После подстановки, имеем:
Равенство корректно, а значит, и деление выполнено верно.
Деление с остатком
Содержание
И так, мы уже познакомились с тем, что же такое деление. Но есть еще один важный и нужный вид деления – это деление с остатком.
Представим, что мы купили 10 яблок. К нам пришли друзья и мы захотели поделиться с ними яблоками, и при этом дать каждому равное количество.
Если друга всего 2, то каждому дадим по 5 яблок; если их 5, то по 2; а если 10, то по одному.
Но что делать, если друзей будет 3, 7 или 9? Нам не получится разделить 10 яблок поровну на такое количество человек.
Откуда берется остаток
Предположим, что в итоге у нас 7 друзей и 10 яблок. Чтобы никого не обидеть, мы можем дать каждому по одному и у нас останется 3 яблока. Теперь давайте рассмотрим пример:
В данном случае, 10 яблок – это делимое, 7 друзей – делитель, а 1 – неполное частное. Что же означает цифра 3 и откуда она взялась?
То число, которое осталось при делении, называют остатком.
Соответственно, в нашем случае 3 яблока и будут остатком.
Как найти остаток
Рассмотрим другой пример:
Запомним еще 2 правила, которые необходимы при работе с остатком:
Остаток всегда меньше делителя.
Если остаток равен нулю, то говорят, что делимое делится на делитель без остатка, то есть нацело.
Как найти делимое
Нужно уметь находить не только частное и остаток, но и делимое. На самом деле, здесь также все просто.
Чтобы найти делимое при делении с остатком, нужно умножить неполное частное на делитель и к полученному произведению прибавить остаток.