Как решать буквенные задачи
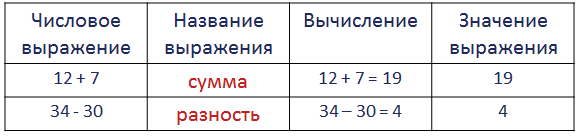
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
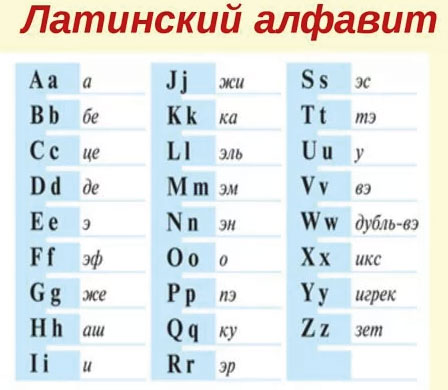
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях:
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 25. Буквенные выражения
Перечень вопросов, рассматриваемых в теме:
— Что такое буквенное выражение?
— Как найти значение буквенного выражения?
Числовое выражение – выражение, составленное из чисел, знаков математических действий и скобок.
Значение выражения – это число, полученное в результате выполнения всех действий в выражении.
Буквенное выражение – выражение, составленное из чисел, букв, знаков математических действий и скобок.
Переменная – это значение буквы в буквенном выражении.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
Теоретический материал для самостоятельного изучения
Вы уже умеете решать примеры «с окошками». 5 + = 8
Мы подбираем число, чтобы равенство было верным. Это число 3. Подставим вместо «окошка» это число. Получим равенство: 5 + 3 = 8
Кроме равенства, вы умеете решать «с окошком» и неравенства. Мы подбираем число или числа, чтобы неравенство было верным. 5 + > 8
Это могут быть любые числа, больше числа 3.
С «окошками» можно записывать и просто выражения:
«сумма числа четыре и неизвестного числа», 4 +
«разность неизвестного числа и числа три». — 3
Вместо «окошка» в математике записывают латинские буквы.
Запишем выражение с буквой «a»: 5 + а
Выражение с буквами называется «буквенное выражение»
Чаще всего используют маленькие латинские буквы:
Вместо буквы, как и вместо «окошка» можно подставлять различные числа и находить значения выражений. Посмотрите, как можно заменить букву числом в выражении 6 + d.
Заменим букву числом в выражении: а – 7. Посмотри, как это сделать.
Обратите внимание, что если буква – это уменьшаемое, то мы не можем заменить её любым числом.Оно должно быть обязательно больше или равно вычитаемому.
Так, для выраженияа – 7, значение переменной а равно:
Заменим букву числом в выражении: 4 – с. Посмотри, как это сделать.
Обратите внимание, что если буква – это вычитаемое, то мы не можем заменить её любым числом. Оно должно быть обязательно меньше или равно уменьшаемому.
Так, для выражения 4 – с, значение переменной с равно:
Вывод: Буквенным выражением называется выражение, состоящее их чисел, букв латинского алфавита, знаков действий. Число, полученное в результате выполнения всех действий после подстановки чисел вместо букв, в числовом выражении называют значением этого выражения. Значение этого выражения будет зависеть от того, какими будут значения этих букв – переменных
1.Зачеркните числа, которые нельзя поставить вместо переменной в выражение
а – 8 12, 45, 6, 34, 7, 10, 8, 4, 56
12, 45, 6, 34, 7, 10, 8, 4, 56
2. Восстановите алгоритм решения буквенных выражений
Алгоритм решения буквенных выражений
Алгоритм решения буквенных выражений
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Урок математики: «Буквенные выражения» (2-й класс)
Класс: 2
Ход урока
1. Организационный момент
а) 2 человека получают карточки и начинают работать на закрытых крыльях доски.
1 карточка:
Выпиши только суммы и найди их значения.
60 – 36 = 70 – 7 = 57 + 3 = 72 – 4 = 27 + 5 = 66 + 30 =
2 карточка:
Выпиши только разности и найди их значения.
60 – 36 = 70 – 7 = 57 + 3 = 72 – 4 = 27 + 5 = 66 + 30 =
б) Разминка, включение в работу.
Ответьте на мой вопрос: Зайчата спрятались от волка. Из-за кустика видно 8 ушек. Сколько зайчат спряталось за кустиком?
60 – 36 = 70 – 7 = 57 + 3 = 72 – 4 = 27 + 5 = 66 + 30 =
Вначале прочитайте и вычислите только суммы (Прочитайте по-разному: а) 1 слагаемое, 2 слагаемое, сумма; б) сумма чисел…; в) к 57 прибавить 3)
Покажите ответы карточками.
Теперь прочитайте и вычислите только разности (Прочитайте по-разному: 1) уменьшаемое, вычитаемое, разность; 2) из 70 – 7)
Показывайте ответы карточками.
Как называются такие выражения? (числовые)
А какие еще бывают выражения? (буквенные)
Почему они так называются? (В их записи используются латинские буквы)
Какой же будет тема сегодняшнего урока? (Буквенные выражения)
а) с.6 №4 (на экране: слайд 3)
d 6 7 8 9 10 d – 5 1 d + 10 16
d – 5 и d + 10 – Что это? (Буквенные выражения)
– Как вычислить решить такое буквенное выражение? (Вместо буквы можно подставить любое число)
– Как получили число 1? (Букву d заменили числом 6. Получилось выражение 6 – 5. Разность равна 1)
– Как получить следующее число 2-ой строки? (d = 7, 7 – 5 = 2)
Аналогично закончить строку.
– Как получили число 16? (Букву заменили числом 6. Получилось выражение 6 + 10. Сумма равна 16)
Как получить следующее число 3-ей строки? (в = 7, 7 + 10 = 17)
Аналогично закончить строку.
б) с.6 №5 Самостоятельная работа.
– Прочитайте. Что надо сделать сначала? (Записать сумму и разность)
– Что будем делать дальше? (Подставлять числа вместо буквы)
а = 12 12 + 8 = 20 12 – 8 = 4
Закончите задание самостоятельно. Проверьте выполнение в парах.
Упражнение для глаз (слайд 4)
а) А сейчас вы попробуете подобрать буквенные выражения к схемам задач. (Используются карточки Кларо) Работать будете парами. Один ученик работу выполняет на компьютере (экран закрыт).
Проверьте себя, сверив свою работу с изображением на экране. (слайд 5)
б) с.6 №8. Решение задачи.
– О чем задача? (О книгах.)
– Где стояли книги? (На полках)
– Сколько было полок? (Две)
– Что известно о книгах на каждой из полок? (На одной – 32 книги, на второй – 40 книг.)
– Что сделали с книгами? (Выдали читателям.)
– Сколько книг выдали? (20 книг).
– Посмотрите макет задачи.
(Макет выполнен из кирпичиков ЛЕГО).
 |  |
(Я выставила 3 одинаковых макета, что должно натолкнуть на мысль о нескольких способах решения задачи.)
– Решите задачу самостоятельно. Каждый может решить задачу по-своему.
(В процессе решения учитель вызывает к доске 3-х учеников, которые решили задачу разными способами.)
– Давайте сверим свое решение с решением на доске. Все решения разные. Какое из них правильное? Докажите, что ваше решение верное, используя макеты. (Каждый ученик у доски объясняет свое решение.)
– Запишите три способа решения выражениями. Сверьтесь с записью на экране (слайд 6).
– Всегда ли такую задачу можно решить 3-мя способами? (Да. Нет)
– Мнения разделились. Поясните свой ответ, те кто считает, что 3-мя способами решить задачу можно не всегда.
– После обсуждения, приходим к выводу:
Если количество книг больше 32, то задачу можно решить 2-мя способами. Если количество книг будет больше 40, то задачу можно будет решить только одним способом.
– Чему учились на уроке? (Учились решать буквенные выражения, решали задачу разными способами)
– Кто научился решать буквенные выражения? А кто не уверен в своих знаниях?
– Что узнали нового? (Узнали, что если изменятся данные задачи, то и количество способов решения тоже может измениться.)
Урок 15 Бесплатно Числовые и буквенные выражения
Любые математические задачи и примеры записываются с помощью математического языка.
Математический язык- это язык, не требующий перевода, универсальный и понятный всем, имеющий четкую структуру и грамматику.
Верная математическая запись всегда точна, логична, компактна, удобна для понимания, однозначно отражает действие, операцию, понятие.
Определенная осмысленная последовательность знаков (чисел, букв), связанных между собой знаками арифметических операций, называют математическим выражением.
Математические выражения делят на числовые и буквенные.
На этом уроке вы познакомитесь с числовыми и буквенными выражениями.
Узнаете, какое выражение называют числовым, а какое буквенным.
Научитесь составлять числовые и буквенные выражения к задачам.
Выясните, как правильно записывать, читать и находить значение математических выражений.
Числовые выражения
Числовые выражения вам уже хорошо знакомы.
В начальных классах на уроках математики, решая задачи и примеры, вы составляли и записывали числовые выражения и находили значения этих выражений.
Числовое выражение- это запись, состоящая из чисел, арифметических операций, скобок и иных специальных математических символов.
Числовым выражением можно назвать только такую запись, которая является осмысленной и составлена согласно математическим правилам.
Рассмотрим примеры числовых выражений.
Не каждую математическую запись из символов и знаков можно считать числовым выражением.
Числовое выражение всегда ориентировано на то, чтобы операции, входящие в него, могли быть выполнены.
Если числовое выражение невозможно вычислить, то оно не имеет смысла.
Существуют такие математические записи, которые на первый взгляд можно принять за числовые выражения, но вычислить их невозможно.
Число 15 необходимо разделить на результат операции в скобках, а он равен нулю.
Математические равенства и неравенства выражениями не являются, но равенства и неравенства состоят из математических выражений.
Два числовых выражения, соединенные знаком равно «=», называют числовым равенством.
Два числовых выражения, соединенные знаками больше «>» или меньше « 4 не является числовым выражением, это неравенство.
Смысл решения любой задачи, любого примера заключается в том, чтобы найти значение выражения, которое превращает его в верное равенство.
Число, которое получается после выполнения всех арифметических операций, называют значением числового выражения.
Следовательно, чтобы найти значение числового выражения, необходимо выполнить в определенном порядке все арифметические операции, указанные в выражении.
У числового выражения значение только одно.
У меня есть дополнительная информация к этой части урока!
Порядок выполнения математических операций очень важен для получения верного значения числового выражения.
В математике порядок выполнения действий в выражении определяют сами арифметические операции и скобки, содержащиеся в данном выражении.
Таким образом, если в числовом выражении стоят скобки, то математическая операция, стоящая в них, выполняется в первую очередь.
Следующими выполняются последовательно слева направо операции умножения и деления, если такие присутствуют в выражении.
Последними выполняются действия сложения и вычитания так же в порядке их следования друг за другом слева направо.
Более подробно порядок выполнения арифметических операций будет рассмотрен несколькими уроками позже.
Важно уметь не только верно записывать числовые выражения, но и уметь их правильно читать.
Чтобы прочитать числовое выражение нужно определить, какая арифметическая операция является последней при вычислении значения этого выражения.
Так, например, если последнее по порядку действие было сложение, то выражение называют «суммой».
Если последним действием является вычитание, то выражение называют «разностью».
Следовательно, если последним действием является умножение, то выражение называют «произведением», если деление- «частным».
Умение составлять математические выражения и находить их значение используют при решении как простых, так и составных задач.
Рассмотрим пример решения составной задачи и выясним особенности процесса составления числовых выражений.
Известно, что любая составная задача содержит несколько простых.
Существуют различные способы оформления решения текстовых задач.
Чаще всего используют такие формы записи решения задач:
1. По действиям с пояснениями.
При решении составных задач важно выделить главное, сделать краткую запись, разделить задачу на простые, составить план решения.
В первый день собрали 12 кг клубники, а во второй день на 2 кг больше.
Сколько килограммов клубники собрали за эти два дня?
Запишем кратко условие задачи:
Изобразим к задаче рисунок в виде схемы.
Чтобы определить, сколько собрали клубники за два дня, необходимо знать, какое количество клубники было собрано в первый и во второй день.
Из условия задачи известно количество клубники, собранной в первый день.
Неизвестно количество клубники, собранной во второй день.
Когда будет известно сколько собрали клубники во второй день, можно узнать какое количество ягод собрали за два дня.
Задачу решаем в два действия (каждое действие поясним).
1. Выясним сколько килограммов ягод собрали во второй день.
Известно, что в первый день собрали 12 кг клубники. Так как во второй день собрали на 2 кг больше, то во второй день собрали столько же, как в первый, и еще 2 кг.
Выполним сложение чисел 12 и 2, получим выражение 12 + 2.
Найдем значение данного числового выражения:
12 + 2 = 14 (кг) клубники собрали во второй день.
2. Вторым действием определим общее количество ягод, собранных за два дня.
Необходимо сложить все ягоды, который собрали в первый и во второй день, получим следующее выражение: 12 + 14.
Найдем значение данного числового выражения:
12 + 14 = 26 (кг) клубники собрали за два дня.
Ответ: 26 кг.
Как нам уже известно, решение задачи можно записать не только по действиям, но и в форме выражения.
Запись решения составной задачи с помощью составления по ней итогового числового выражения позволяет увидеть ход решения в целом, и такая запись сокращает время оформления задачи.
Составим числовое выражение для решения нашей задачи.
Согласно рассуждениям, изложенным выше, имеем следующие данные:
Определим общее количество ягод, собранных за два дня.
Сложив все ягоды, собранные в первый и во второй день, получим следующее числовое выражение:
12 + (12 + 2).
Вычислим значение данного выражения, выполнив последовательно все действия в нем.
Тогда запись решения задачи будет выглядеть так:
12 + (12 + 2) = 12 + 14 = 26 (кг) клубники собрали за два дня.
Ответ: 26 кг.
Попробуем решить вторую задачу.
Задача 2.
В первый день собрали 12 кг клубники, а во второй день на 5 кг больше.
Сколько килограммов клубники собрали за эти два дня?
Скорее всего вы заметили, что первая и вторая задачи отличаются только одним числом, а именно число 2 заменено на число 5.
Остальные условия задачи остались прежние.
Все логические рассуждения во второй задаче аналогичны рассуждениям первой.
Таким образом, имеем следующие данные:
Определим общее количество ягод, собранных за два дня.
Сложив все ягоды, собранные в первый и во второй день, получим следующее выражение:
12 + (12 + 5).
Вычислим значение данного выражения, выполнив последовательно все действия в нем.
Тогда запись решения задачи будет выглядеть так:
12 + (12 + 5) = 12 + 17 = 29 (кг) клубники собрали за два дня.
Ответ: 29 кг.
Пройти тест и получить оценку можно после входа или регистрации
Буквенные выражения
Рассмотрим еще одну такую же задачу, как первая и вторая, рассмотренные выше, но число, которое менялось в первой и во второй задаче заменим на ☐ пустое окошко, в которое можно вписать любое значение.
Тогда получим следующую задачу:
В первый день собрали 12 кг клубники, а во второй день на ☐ кг больше.
Сколько килограммов клубники собрали за эти два дня?
В математике принято обозначать переменное число не пустым окошком, а буквой.
Для нашей задачи вместо пустого окошка поставим латинскую букву «а».
По аналогии с уже решенными задачами математическое выражение для данной задачи будет следующее: 12 + (12 + а).
Если вместо буквы а подставлять различные числа, то каждый раз будем получать различные числовые выражения и, как следствие, различные значения.
Числовое выражение, в котором числа обозначены цифрами и буквами, называют буквенным выражением.
Соответственно, буквенное выражение отличается от числового тем, что содержит букву.
Буквы, которые содержатся в буквенных выражениях, называются переменными.
Для обозначения чисел буквами используют строчные буквы латинского алфавита.
Буквенные выражения должны быть составлены согласно математическим правилам и по такому же принципу, как числовые выражения.
1. Буквенные выражения используют для математических доказательств, для описания свойств, правил, законов.
Например, переместительное свойство сложения, записанное с помощью буквенных выражений, выглядит так: a + (b + c) = (a + b) + c.
Сочетательное свойство сложения, записанное с помощью буквенных выражений, выглядит так: a + b = b + а.
2. Правило, записанное в виде равенства двух буквенных выражений, называется формулой.
Формула подобно универсальной заготовке позволяет описывать различные процессы, действия, состояния и др.
Формула устанавливает взаимосвязь между величинами.
Например, формула для определения периметра треугольника, записанная с помощью буквенных выражений, выглядит так: P = a + b + c, где
P— это периметр треугольника
а, b, c— это стороны треугольника.
В данном случае буквенная запись позволяет определить периметр (Р) любого треугольника, независимо от размеров его сторон.
3. Умение составлять буквенные выражения и находить их значения при заданном значении переменной используют при решение различных задач
Пройти тест и получить оценку можно после входа или регистрации