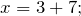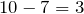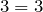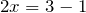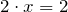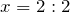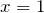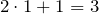Как решать алгоритмические уравнения

Алгоритмы

Алгоритмы. Разработка алгоритма решения задачи

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

,

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

В тело цикла входят:

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

© 2015-2021 Университетский центр компьютерного обучения «Турбо»
г. Майкоп, ул. Ветеранов, 228, тел.: 8 (8772) 57-11-00, 8(918)213-95-94

Источник

Решение простых линейных уравнений

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие уравнения

Понятие уравнения обычно проходят в самом начале школьного курса алгебры. Его определяют, как равенство с неизвестным числом, которое нужно найти.

В школьной программе за 7 класс впервые появляется понятие переменных. Их принято обозначать латинскими буквами, которые принимают разные значения. Исходя из этого можно дать более полное определение уравнению.

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядит так

ах + b = 0, где a и b — действительные числа. Что поможет в решении: Система уравнений — это несколько уравнений, для которых нужно найти значения неизвестных. Она имеет вид ax + by + c = 0 и называется линейным уравнением с двумя переменными x и y, где a, b, c — числа. Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому выражению и является верным числовым равенством. Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравнения Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте схему-подсказку — храните ее в телефоне, учебники или на рабочем столе. А вот и видео «Простейшие линейные уравнения» для тех, кто учиться в 5, 6 и 7 классе. Примеры линейных уравнений Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х — 3) + 2 = 3 (х — 4) + 2х — 1. 5х — 15 + 2 = 3х — 2 + 2х — 1 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 — 7х. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 — 7х.. Источник Алгоритм решения уравнений. Алгоритм решения уравнений 7 класс.Решение линейных уравнений по алгоритму. Просмотр содержимого документа «Алгоритм решения уравнений.» 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) 2. Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.(при переносе меняем знак на противоположный) 3. Привести подобные слагаемые в каждой части уравнения. 4. Разделить обе части уравнения на коэффициент при неизвестном. (Примечание: часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. ) Источник Алгоритм решения уравнений Решить уравнение — это значит найти неизвестную величину, после подстановки которой в уравнение получаем верное равенство. Алгоритм решения уравнения Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность Чтобы найти неизвестный множитель, надо произведение поделить на известный множитель Чтобы найти неизвестное делимое, необходимо частное умножить на делитель Чтобы найти неизвестный делитель, надо делимое поделить на частное Примеры решения задач Задание Решить уравнение 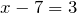Решение 1) Записываем уравнение: 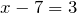; 2) данное уравнение на нахождение разности; 3) неизвестным является уменьшаемое. 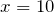Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое: 4) ; 5) сделаем проверку, для этого подставим полученное значение 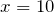в исходное уравнение: Получили верное равенство, корень найден верно.

Ответ

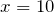
Задание	Решить уравнение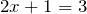
Решение	Заданное уравнение содержит неизве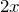стное слагаемое , чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое:

Получили простейшее уравнение на нахождение произведения. Чтобы найти неизвестный множитель, надо произведение поделить на известный множитель:

— верное равенство.

Ответ

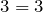
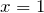
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.

Источник

Алгоритмы решения простых и усложнённых уравнений в начальной школе.

Решить уравнение – найти его корень:

— записывается строго в столбик

— в каждой строке только один знак = так как получаться должны равенства

— после нахождения корня уравнения эту строку подчеркнуть для проверки

— в части проверки не пишется неизвестное, вместо него пишут число – корень уравнения

Алгоритм решения простого уравнения :

1. Подчеркнуть неизвестное и вспомнить как называется компонент действия, на месте которого находится неизвестное число.

2. Вспомнить правило нахождения этого компонента.

3. Решить простое уравнение по озвученному правилу в одно действие.

4. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

5. Записать ответ проверки – посчитать всё в левой части, записать равно под равно, и полученное число левой части написать перед равно. Оно должно получиться таким же, как и число в правой части уравнения.

1. Подчеркнуть неизвестное и вспомнить как называется компонент действия, на месте которого находится неизвестное число

Неизвестен второй множитель.

2. Вспомнить правило нахождения этого компонента.

Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

3. Решить простое уравнение по озвученному правилу в одно действие.

4. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

5. Записать ответ проверки – посчитать всё в левой части, записать равно под равно, и полученное число левой части написать перед равно. Оно должно получиться таким же, как и число в правой части уравнения.

Алгоритм решения усложнённого уравнения :

2. Подчеркнуть неизвестное и вспомнить как называется компонент действия, на месте которого находится неизвестное число

3. Вспомнить правило нахождения этого компонента.

4. Решить простое уравнение по озвученному правилу в одно действие.

5. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

6. Записать ответ проверки – посчитать всё в левой части, записать равно под равно, и полученное число левой части написать перед равно. Посчитать всё в правой части и записать после равно полученное число Оба числа должны получиться равными.

Х + 500 × 3 = 2000 могу 500 ×3, получу 1500

Получим простое уравнение :

2. Подчеркнуть неизвестное и вспомнить как называется компонент действия, на месте которого находится неизвестное число.

Х + 1500 = 2000 неизвестное стоит на месте 1-го слагаемого

3. Вспомнить правило нахождения этого компонента.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

4. Решить простое уравнение по озвученному правилу в одно действие.

5. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

6. Записать ответ проверки – посчитать всё в левой части, записать равно под равно, и полученное число левой части написать перед равно. Посчитать всё в правой части и записать после равно полученное число Оба числа должны получиться равными.

Алгоритм решения сложного уравнения :

5. Решить полученное простое уравнение.

6. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

7. Записать ответ проверки – посчитать всё в правой и левой части, записать равно под равно, должно получиться одинаковое число в правой и левой части.

Пропускаем – нельзя упростить.

Неизвестно уменьшаемое, чтобы найти неизвестное уменьшаемое надо к вычитаемому прибавить разность.

получили простое уравнение, такое уравнение мы умеем решать

Неизвестно слагаемое, чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое.

5. Решить полученное простое уравнение.

6. Выполнить проверку правильности решения – переписать всё уравнение, подставив вместо неизвестного корень уравнения.

7. Записать ответ проверки – посчитать всё в правой и левой части, записать равно под равно, должно получиться одинаковое число в правой и левой части.

Источник