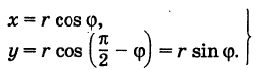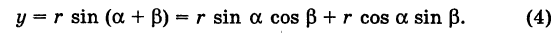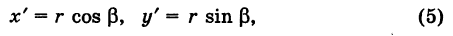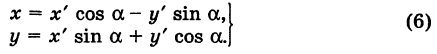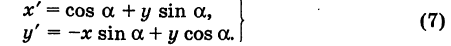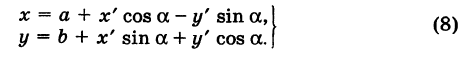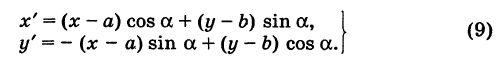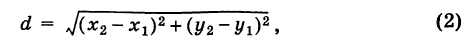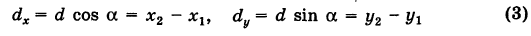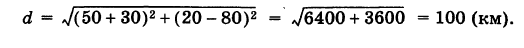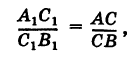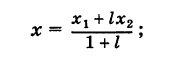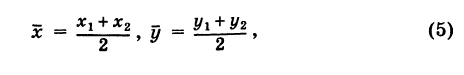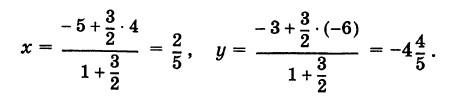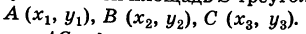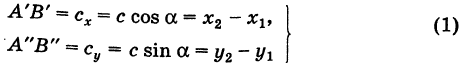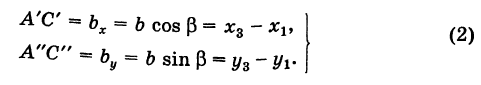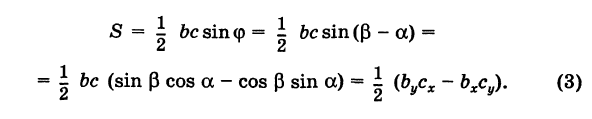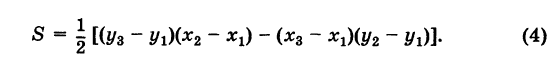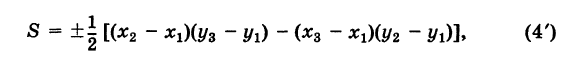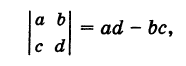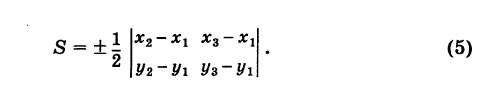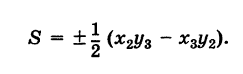Как решается система координат

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

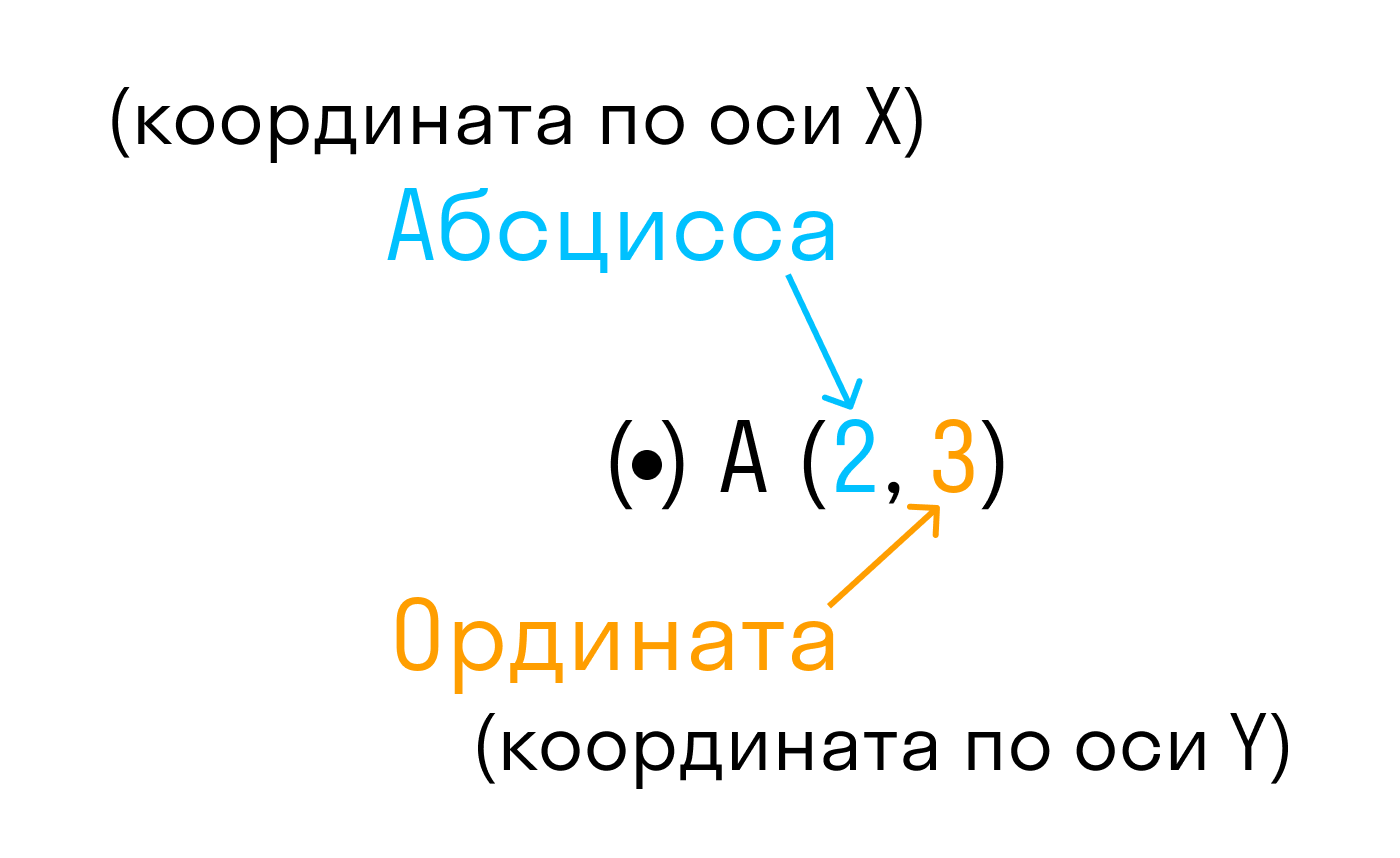
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Источник

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

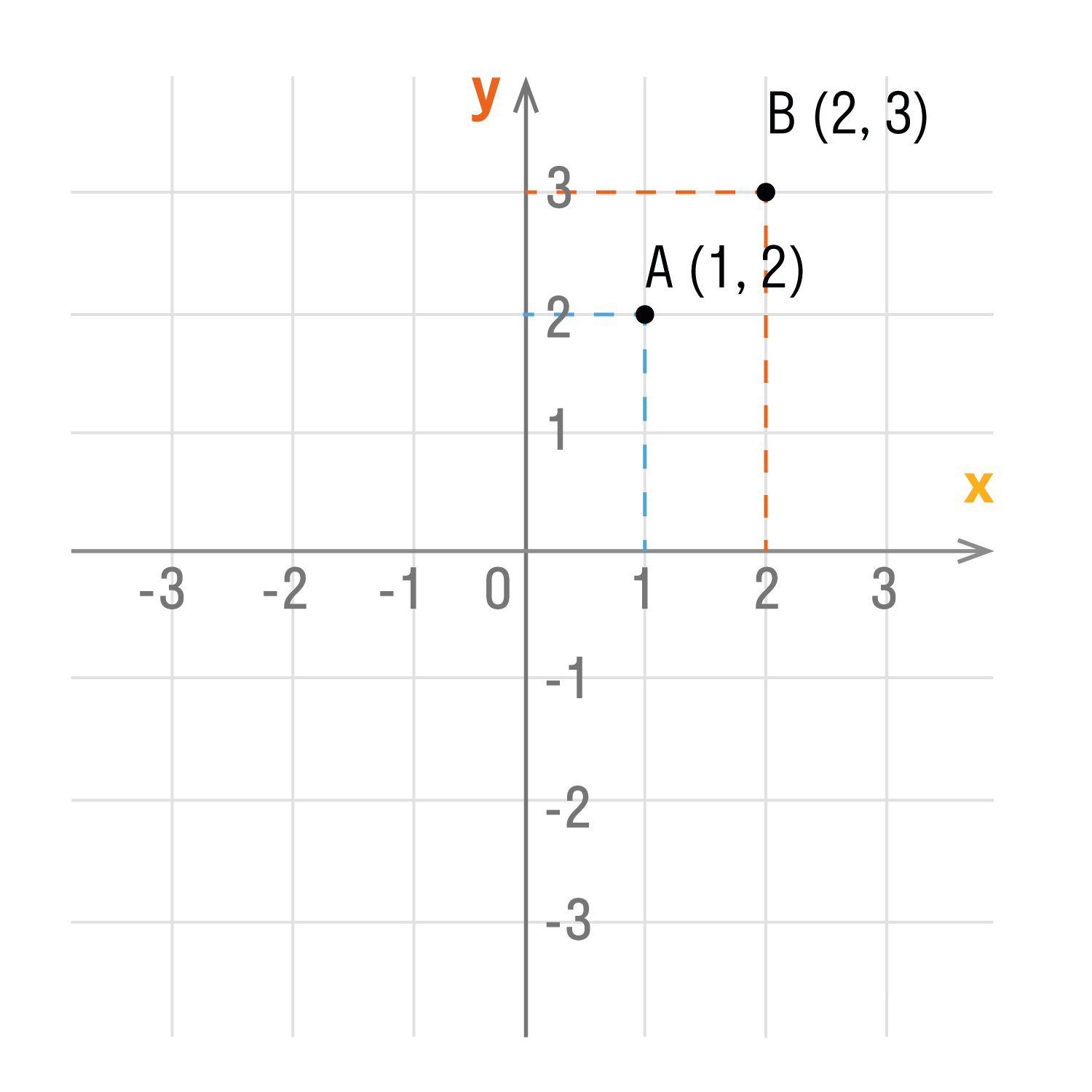
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Система координат

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

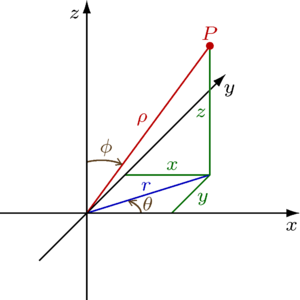
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана). См. Географические координаты.

В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Источник

Система координат

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Содержание

Список наиболее распространённых систем координат

Основные системы

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел :

В пространстве же необходимо уже 3 координаты :

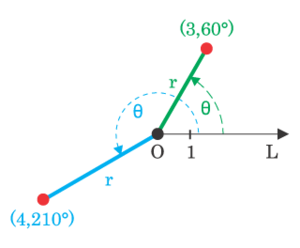
Полярные координаты

В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.

Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.

Цилиндрические координаты

Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем . В терминах декартовой системы координат,

Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение , тогда как в цилиндрических оно выглядит как r = c

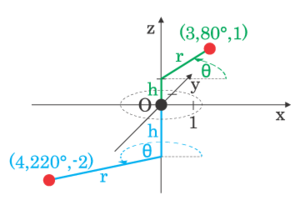
Сферические координаты

Сферические координаты — трехмерный аналог полярных

Обозначения, принятые в Америке

В сферической системе координат, расположение точки P определяется тремя компонентами: . В терминах декартовой системы координат,

Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.

Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.

Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как , тогда как в сферических становится намного проще: .

Европейские обозначения

В Европе принято использовать другие обозначения. Положение точки задаётся числами: , Где r — расстояние от точки до начала координат, — полярный угол, который изменяется в пределах от 0 до π, — Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.

Переход из одной системы координат в другую

Декартовы и полярные

Источник

Прямоугольная система координат на плоскости и ее применение с примерами

Содержание:

Прямоугольная система координат на плоскости и ее применение к простейшим задачам

Прямоугольные координаты точки на плоскости

Координатами точки на плоскости называются числа, определяющие положение этой точки на плоскости.

Прямоугольные декартовы координаты (по имени математика Декарта) на плоскости вводятся следующим образом: на этой плоскости выбираются точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ох и Оу (оси координат) (рис. 1). Для удобства рассмотрения будем предполагать, что ось Ох 0ось абсцисс) горизонтальна и направлена слева направо, а ось Оу (ось ординат) вертикальна и направлена снизу вверх; таким образом, ось О у повернута относительно оси Ох на угол 90° против хода часовой стрелки 1 ). Кроме того, выбирается единица масштаба для измерения расстояний.

Для данной точки М введем в рассмотрение два числа: абсциссу х и ординату у этой точки.

Абсциссой х называется число, выражающее в некотором масштабе расстояние от точки до оси ординат, взятое со знаком плюс, если точка лежит вправо от оси ординат, и со знаком минус, если точка лежит влево от оси ординат. Ординатой у называется число, выражающее в некотором масштабе (обыкновенно в том же, как и для абсциссы) расстояние от точки до оси абсцисс, взятое со знаком плюс, если точка лежит выше оси абсцисс, и со знаком минус, если точка лежит ниже оси абсцисс.

Эти два числа х и у и принимаются за координаты точки М, так как они полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка, координатами которой являются эти числа; и обратно, каждая точка плоскости имеет определенные координаты х и у. Если точка М имеет координаты х и у, то это обстоятельство обозначают так: М (х, у) (на первом месте ставится абсцисса х, а на втором — ордината у). При записи координат знак плюс, как обычно, можно опускать.

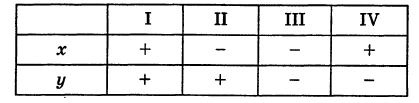
Оси Ох и Оу разбивают плоскость на четыре части, называемые квадрантами. Производя нумерацию квадрантов (I, II, III и IV) в направлении против хода часовой стрелки, отправляясь от того квадранта, где обе координаты положительны, получим следующую таблицу знаков координат:

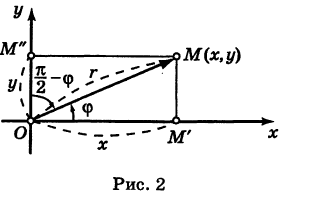
Отрезок ОМ у соединяющий начало координат О с точкой М (рис. 2), называется ее радиусом-вектором. Обозначая через ф угол, образованный отрезком ОМ с положительным направлением оси Ох, и через 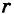его длину, для точки М, лежащей в I квадранте, из треугольников ОММ’ и ОММ» получим

Нетрудно убедиться, что формулы (1) будут справедливы для координат точек всех квадрантов. Таким образом, знак абсциссы х точки М совпадает со знаком косинуса, а знак ее ординаты у — со знаком синуса в соответствующем квадранте.

Легко видеть, что если точка лежит на оси абсцисс, то ее ордината у равна нулю; если же она лежит на оси ординат, ее абсцисса х равна нулю, и обратно. Следовательно, если точка совпадает с началом координат, то равны нулю обе ее координаты.

В дальнейшем прямоугольные декартовы координаты для краткости будем называть просто прямоугольными координатами.

В следующих параграфах рассмотрим некоторые простейшие задачи на применение прямоугольных координат на плоскости.

Преобразование прямоугольной системы координат

При решении задач иногда выгодно вместо данной прямоугольной системы координат выбрать другую прямоугольную систему координат О’х’у определенным образом ориентированную относительно первой. Например, при межпланетных путешествиях можно пользоваться системой координат, связанной с центром Земли (геоцентрическая система координат); однако более удобно использовать систему координат, связанную с центром Солнца (гелиоцентрическая система координат).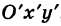

Возникает вопрос о том, как от одной системы координат перейти к другой.

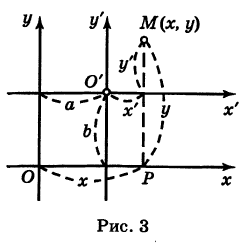
Рассмотрим сначала простейший случай (рис. 3), когда оси «новой системы координат» О’х’у’ параллельны соответствующим осям «старой системы координат о Оху и имеют одинаковые направления с ними (параллельный перенос системы координат).

Пусть начало новой системы координат — точка О’ — имеет координаты (а, Ь) в старой системе координат. Точка М плоскости со «старыми координатами» (х, у) будет иметь некоторые «новые координаты» [х\ у’] (для ясности мы их обозначаем квадратными скобками). Из рис. 3 непосредственно получаем

т. е. новые координаты точки равны ее старым координатам минус старые координаты нового начала.

Обратно, из (1) находим

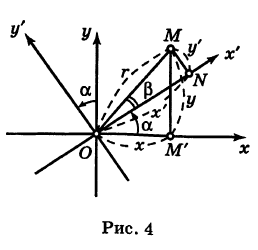
Пусть теперь «новая система» координат Ох’у\ при неизменном начале О, повернута относительно «старой системы» Оху на угол а (рис. 4), т. е. 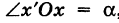, причем а считается положительным, если поворот осуществляется против хода часовой стрелки, и отрицательным — в противоположном случае (поворот системы координат).

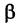
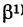
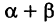
Обозначим через угол, образованный радиусом-вектором г = ОМ точки М с осью Ох’; тогда отрезок ОМ, с учетом знака угла ), будет составлять с осью Ох угол . Отсюда на основании формул (1) из при любом расположении точки М имеем

Так как новые координаты точки М, очевидно, есть

то из формул (3) и (4) получаем

Для запоминания формул (6) используют следующий мнемонический прием: говорят, что первая формула (6) содержит полный беспорядок, а вторая — полный порядок. Действительно, в первой формуле на первом месте стоит cos, на втором — sin; кроме того, присутствует знак минус. Во второй формуле (6) никаких нарушений правильности в этом смысле нет.

Наконец, в общем случае, когда новое начало координат есть точка О’ (a, Ь) и ось О’х’ образует с осью Ох угол а, соединяя формулы (2) и (6), находим

Здесь угол Р считается положительным, если радиус-вектор ОМ повернут относительно оси Ох’ против хода часовой стрелки, и отрицательным, если он повернут относительно этой оси по ходу часовой стрелки.

Аналогично, из формул (1) и (7) получаем

Из формул (8) и (9) вытекает, что формулы перехода от одной прямоугольной системы координат к другой прямоугольной системе координат являются линейными функциями как новых, так и старых координат, т. е. содержат эти координаты в первой степени.

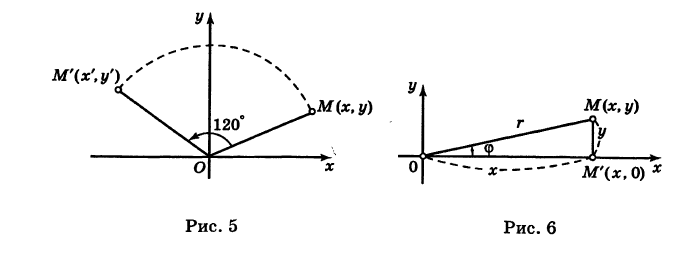
Пример:

Отрезок ОМ, где точка М имеет координаты (х, г/), повернут на угол а = 120° против хода часовой стрелки (рис. 5). Каковы будут координаты х’ и у’ нового положения М’ точки М?

Решение:

Предполагая, что с точкой М связана подвижная система координат Ох’у\ на основании формул (6) будем иметь

Расстояние между двумя точками на плоскости

1) Найдем сначала расстояние г от начала координат О (0, 0) до точки М (х, у) (рис. 6).

Расстояние г = ОМ, очевидно, является гипотенузой прямоугольного ОММ’ с катетами . По теореме Пифагора получаем

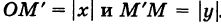
Таким образом, расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки.

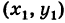
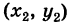
2) В общем случае, пусть для точек A и Б (рис. 7) требуется найти расстояние d = АВ между этими точками.

Выберем новую систему координат Ах’у’ начало которой совпадает с точкой А и оси которой параллельны прежним осям и имеют, соответственно, одинаковые направления с ними. Тогда в новой системе координат точки Л и В будут иметь координаты А [0, 0] и Б 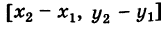. Отсюда на основании формулы (1) получаем

т. е. расстояние между двумя точками плоскости (при любом их расположении) равно корню квадратному из суммы квадратов разностей одноименных координат этих точек.

Замечание. Формула (2) дает также длину отрезка АВ. Легко определить направление этого отрезка. Из прямоугольного А ABC имеем

(dx и dy называются проекциями отрезка АВ на оси координат Оху). Отсюда получаем 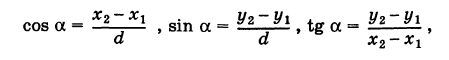где d определяется формулой (2).

Пример:

Танк на местности переместился из точки А (-30, 80) в точку Б (50, 20) (относительно некоторой системы координат Оху)> причем координаты точек даны в километрах. Найти путь d, пройденный танком, если он двигался, не меняя направления.

Решение:

Применяя формулу (2), имеем

Деление отрезка в данном отношении

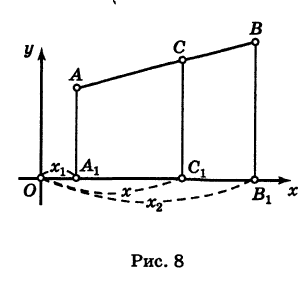
Предположим, что отрезок АВ (рис. 8), соединяющий точки A (xl9 уг) и В (x2t у2), разделен точкой С на два отрезка АС и СБ, причем отношение АС к СБ равно I (I > 0):

Требуется выразить координаты х и у точки С(х, у) через координаты концов отрезка АВ.

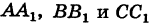
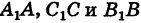
Опустим перпендикуляры соответственно из точек А, В и С на ось Ох. Тогда получим, что три параллельные прямые пересекают стороны угла (не обозначенного на рисунке), образованного прямыми АВ и Ох. Как известно из элементарной геометрии, пучок параллельных прямых рассекает стороны угла на пропорциональные части; поэтому

откуда на основании равенства (1) будем иметь

Решая уравнение (3) относительно неизвестной абсциссы х, будем иметь

Итак, координаты точки С (ху у), делящей отрезок АВ в отношении / (считая от А к В), определяются формулами Если точка С делит отрезок АВ пополам, то АС = СВ и, следовательно, I = АС/СВ = 1. Обозначая координаты середины отрезка АВ через х, у, получим на основании формул (4)

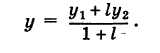
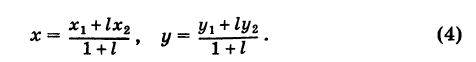
т. е. координаты середины отрезка равны полусуммам соответствующих координат его концов.

Примечание. При выводе формул (4) и (5) мы предполагали, что концы А и В отрезка АВ лежат в первом квадранте и, следовательно, координаты точек Аи В положительны. Легко доказать, что формулы (4) и (5) будут справедливы и в случае произвольного расположения отрезка АВ на координатной плоскости.

Пример:

Решение:

В этом случае I = 3/2 и, следовательно,

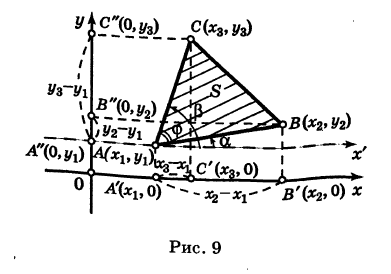
Площадь треугольника

Пусть требуется найти площадь S треугольника ABC (рис. 9) с вершинами

Пусть АВ = с, АС = Ь, а углы, образованные этими сторонами с осью Ох, соответственно равны .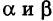

На основании (см. замечание) имеем (рис. 9)

и

Пусть ; очевидно (рис. 9), . По известной формуле тригонометрии получаем

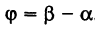
Отсюда в силу (1) и (2) имеем

Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус. Поэтому формулу для площади треугольника обычно пишут в виде

где знак выбирается так, чтобы для площади получалось положительное число,

Используя понятие определителя второго порядка

формулу (4′) можно записать в удобной для запоминания форме:

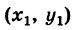
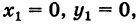
Формула (4′) упрощается, если точка А находится в начале координат. А именно, полагая получим

Отметим, что если точки А, В, С находятся на одной прямой, то площадь S = 0; и обратно, если S = 0, то вершины А, Б и С расположены на одной прямой.

Пример:

По формуле (5) имеем

Замечание. Вычисление площади многоугольника сводится к вычислению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по формуле (4).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник