Как расшифровать aes 128

AES — американский стандарт шифрования. Часть I

Эта публикация вызвана необходимостью дать возможность обучаемым изучать и моделировать процессы шифрования/расшифрования и дешифрования последнего стандарта США. Ознакомление с имеющимися публикациями в сети не соответствуют программе обучения в силу их поверхностного подхода, неполноты изложения, и отсутствия должной строгости. Например, нигде не встречается выбор и задание примитивного элемента, формирующего поле, без чего работу и подготовку специалиста, особенно криптоаналитические явления и процессы, организовать и моделировать невозможно. В этой работе используется описание, несколько отличное от оригинала AES, представленного FIPS PUB 197. Здесь описывается шифр AES, с использованием матриц над GF(2 8 ), но примечания работы сохраняются, т. е. шифр реализуется над конечным расширенным полем GF (2 8 ). На русском языке достаточно полная и доступная версия шифра изложена Зензиным О.С. и Ивановым М.А.

Математические основы стандарта шифрования AES США

AES – блочный шифр с длиной блоков равной 128 битам, и шифр поддерживает ключи длиной , равной 128, 192 или 256 бит. AES – это шифр с итерационным ключом: состоит из повторного применения раундового преобразования состояния блока State шифруемого текста. Число раундов шифра обозначается зависит от длины ключа ( для ключа 128 битов, для ключа 192 бита и для ключа 256 бит).

Шифр AES преобразует исходное состояние блока, обозначаемое символом S (State) и принадлежащее множеству матриц (то есть S є – матрица 4 × 4 байта, с ее элементами (коэффициентами) в GF (2 8 )), к другому шифрованному состоянию в .

Пример 1. Блок данных длиной в 128 = 4·32, 4 слова по 32 разряда представляется квадратной таблицей байтов из 4-х строк и 4-х столбцов. Каждая строка содержит байты из 4-х разных 32 разрядных слов, а столбец – байты одного и того же 32-разрядного слова. Весь квадрат образован 4×4 = 16 байтами, которые могут обрабатываться как самостоятельные единицы.

Представление данных, выбранное для элементов поля GF(2 8 )

. Для удобства и лучшего понимания изучаемого материала, а для уяснения деталей выполнения вычислений с карандашом в руках ниже приводятся многочисленные числовые примеры и следующая таблица 1.

Таблица 1. Соответствие десятичных, шестнадцатеричных, двоичных чисел и многочленов

В работе используются четыре представления для обозначения каждого элемента расширенного поля в GF(2 8 ), которые являются эквивалентными одно другому.

Представление данных, используемых в шифре AES

Выберем десятичное целое число, эквивалент которого будем представлять
различными формами в других системах счисления:

1. 212₁₀, десятичным видом – числом в 10-ой системе счисления.

2. <11010100>b, представление элементов сообщения двоичным вектором – элементом векторного пространства GF(2 8 ) двоичных векторов,

3. , многочленное представление – элементом поля Галуа GF [2 8 ], соответствующим двоичному вектору,

4. ₁₆, – шестнадцатеричное представление – числом в 16-системе счисления,

⊕ – операция поразрядного суммирования векторов из GF(2 8 ) по mod2 (без переноса 1 в старший разряд).
⊗ – операция умножения элементов (векторов, многочленов, чисел) из поля GF(2 8 )

Алгоритм стандарта AES и шифра RIJNDAEL оперирует с байтами информации, которые отождествляются с элементами конечного поля Галуа GF(2 8 ). Степень расширения простого поля GF(2) равна 8. Все элементы расширенного поля при представлении их многочленами имеют показатель степень не более семи (≤ 7).

Достигается такое положение приведением всех результатов действий с элементами поля по модулю неприводимого многочлена степени 8, который является формирующим многочленом для этого поля. Кроме неприводимого многочлена для построения поля необходимо задавать примитивный элемент.

В рассматриваемом алгоритме примитивный элемент задан (его порядок должен быть равен порядку мультипликативной группы поля), а многочлен фиксирован и имеет вид φ(x). Не располагая этими характеристикам, работать со стандартом не получится

или 1 <1b>в 16-ричной форме.
Шестнадцатеричная запись неприводимого многочлена 1 <1b>использует 9 разрядов и многочлен φ(x) не принадлежит полю GF(2 8 ).
Таблица П1 представления элементов поля GF(2 8 ) (в конце текста в Приложении).
В таблице П1 размещены все элементы поля в порядке возрастания показателя степени примитивного элемента (α = 00000011₂ = 3₁₀), мультипликативный порядок которого равен 255.

Рассмотрим примеры выполнения арифметических операций над элементами поля при различных представлениях этих элементов. Любой байт исходного текста (элемент поля) формально можно представить строкой символов , коэффициентов двоичного вектора в виде:

Пример 2. Элемент расширенного поля GF(2 8 ) задан в виде двоичного вектора:

Описание многочленом этого элемента имеет вид:

Если доопределить значения ai двоичными значениями, i = 0(1)7, например, так = <11000001>₂, то получим многочлен

так как

Шестнадцатеричное представление этого элемента α₁₆ = <с1>=<11000001>, а десятичное

α₁₀ = = 128 + 64 + 1 = 193₁₀.

Суммирование элементов поля GF(2 8 )

Сложение в рассматриваемом поле представляет операцию поразрядного суммирования значений разрядов слагаемых без переноса единицы в старший разряд. Это операция исключающего ИЛИ (EXOR – EXLUSIV OR) часто обозначается просто XOR. В модулярной арифметике такое сложение называется суммированием по модулю два (mod2).

Пример 3. Выберем в качестве операндов многочлены


Двоичное представление суммы многочленов по модулю два имеет вид
[A(x)⊕B(x)]mod2 = <11000001>⊕ <00001101>= <11001100>;

Представление многочленами

Заметим, что при сложении операндов степень многочлена результата не
увеличивается, и необходимость приведения его по модулю неприводимого многочлена поля φ(x) не возникает. Коэффициенты результата приводятся по модулю два, т. е. все четные коэффициенты обращаются в нуль.

В полях характеристики 2 действия сложения и вычитания операндов равнозначны. Для каждого элемента поля в аддитивной группе обратным к нему (противоположным) является он сам. Так, для элемента (а) противоположным является (-а), так как а + (-а) = 0. Нулевой элемент (единица аддитивной группы поля, нейтральный элемент) в шестнадцатеричном виде – это <00>₁₆.

Умножение элементов поля GF(2 8 )

Операция обычного умножения операндов (в отличие от модулярного ⊗) обозначается точкой между операндами, или знак умножения вообще опускается, когда не возникает опасности разночтения. Операнды в двоичном представлении умножаются по обычным правилам «столбиком». Будем перемножать те же, что и ранее операнды.

Пример 4. Умножение операндов в двоичном представлении
А(х)· В(х) = ·<0d>

Остаток от деления получает вид двоичного, многочленного и 16-ричного представлений (как элемент поля)
R(x) = 01011 1010₂ = = ₁₆. Старший разряд остатка равен нулю и не учитывается.
Степенное представление здесь не приводим, но по таблице П1 его можно найти.

Остаток от деления на неприводимый многочлен φ(x) в его двоичном представлении результата умножения операндов принимаем в качестве произведения операндов как элементов поля GF(2 8 ).

Выполним умножение операндов в представлении многочленами.

Пример 5. Умножение операндов элементов поля в многочленном представлении
А(х) ⊗ В(х) = ⊗ <0d>
A(x) ⊗ B(x) = (moddφ(x),2) =
=(x 10 +(moddφ(x),2) =
=(x 10 +(moddφ(x),2).

Здесь символ (moddφ (x),2) обозначает приведение по двойному модулю: многочлен по модулю φ(x), а его коэффициенты по модулю два, т.е. четные коэффициенты обнуляются. Получившаяся степень (deg(A(x)⊗ B(x)) =10) результата произведения выводит (этот многочлен — результат) за пределы поля. Чтобы результат принадлежал полю, его приводят (редуцируют, делят) по модулю неприводимого многочлена. Выполним такое деление обычным способом (уголком)

Пример 6. Необходимость деления многочленов возникает при
их умножении А(х)⊗В(х)/ φ(x).(Операции деления в поле нет, когда надо что-то поделить, это что-то умножают на обратный элемент делителя в поле)

– остаток отделения на φ(x) принадлежит полю GF(2 8 ), и его принимаем в качестве окончательного результата модулярного умножения.

Наряду с обычным (классическим) рассмотрением операции умножения элементов в двоичном поле существует более удобная схема. Именно такая схема и реализована в стандарте AES.

Рассмотрим сущность этого способа умножения

Пример 7. Другой способ умножения в конечном поле. Пусть задан произвольный многочлен седьмой степени

и значения его коэффициентов .

Умножим его на и получим . Этот результат не принадлежит полю GF(2 8 ) степень его многочлена больше 7 и его необходимо привести по модулю φ(x) = 1<1b>, после чего такое произведение станет элементом поля GF(2 8 ).

С этой целью определяют значение , если то результат уже принадлежит полю, если же , то достаточно вместо деления выполнить лишь вычитание A(x)x – φ(x) или операцию XOR для произведения A(x)x с φ(x).

В этом случае при записи A(x) в сдвиговом регистре умножению на x полинома A(x), т.е. соответствует сдвиг полинома A(x) на один разряд в сторону старших разрядов (влево, т.е. увеличение вдвое) и, если требуется, применяется операция XOR с неприводимым многочленом поля 1<1b>₁₆ =φ(x).

Детализируем все действия. Элемент х в поле GF(2 8 ) имеет представление
x = <02>₁₆=(00000010)₂.
⊗<11>=⊗<10>⊕⊗<01>= α 178 · α 100 ⊕α 178 · α 0 =⊕, так как α 178 · α 100 =α (178+100-255) =α 23 =

Тогда умножение на него приводит просто к сдвигу первого операнда на 1 разряд влево.
⊗ <02>= xtime = 11000001⊗ 00000010= 110000010 — 9-ти разрядное двоичное число. Этот результат выходит за пределы нашего поля. Его возвращают вычитанием неприводимого многочлена поля φ(х), преобразуя в элемент поля. Итоговый результат 10011001 = <99>

⊗ <04>= xtime(99) = 10011001⊗ 00000010 =100110010 — 9-ти разрядное двоичное число. Этот результат выходит за пределы нашего поля. Его возвращают вычитанием неприводимого многочлена поля φ(х), преобразуя в элемент поля. Итоговый результат 00101001 = <29>

Очередной шаг процедуры
⊗ <08>= xtime(29) = 00101001⊗ 00000010 = 0101 0010 = <52>.
Здесь результат не суммируем с φ(x), так как коэффициент .

И еще один шаг
⊗ <10>= xtime(52) = 01010010⊗00000010 = 10100100 = ₁₆.
Здесь также не суммируем с φ(x), так как коэффициент .
Таким образом, найдено значение первого слагаемого в сумме для исходного
выражения, где второе слагаемое равно ₁₆.
Теперь находим окончательно
⊗ <11>= ⊗ <10>⊕ ⊗ <01>= ⊕ =10100100⊕ 11000001 = <65>или

проверка обычным умножением (степенное представление)
A(x)∙ B(x) = ∙ <11>= α 178 ∙α 4 = α 182
(по таблицам находим в строке для α1 182 ) α 182 соответствует <65>₁₆.

Еще большего эффекта при производстве вычислений можно достигнуть, если укрупнить элементы, с которыми выполняются манипуляции. Так в криптоалгоритме RIJNDAEL используются 32-разрядные (4-х-байтовые) слова. Составляющие байт разряды не анализируются по отдельности. Такой подход позволяет 4-байтовому слову в соответствие поставить многочлен А(х) степени не более трех, и коэффициенты которого лежат в поле GF(2 8 ).

Операция умножения таких слов
и
,
где єGF(2 8 ), i = 0(1)3, выполняется по модулю многочлена степени не более четырех. Взятие результата произведения по модулю неприводимого многочлена степени 4 обеспечивает всегда получение результата произведения, как элемента поля.

В качестве такого многочлена выбран многочлен . Он имеет наиболее простую запись, и для него справедливо
.
Последнее свойство оказывается очень полезным при вычислениях.
Для рассматриваемых многочленов операция сложения выполняется аналогично (XOR поразрядное по mod2)
.

Умножение многочленов.
.
Коэффициенты определяются из соотношений
,
,
,
,
,
,
.

Окончательно результатом D(x) умножения ⊗ двух многочленов по модулю будет
, где
,
,
,
,
или более кратко в векторно – матричной записи,

выполним умножение В(х) на х по , учитывая свойства многочлена. Такому умножению, как и ранее, соответствует циклический сдвиг байтов в пределах слова в направлении старшего байта. Так как
, то
x∙(b_3 b_2 b_1 b_0)$» data-tex=»inline»/>
реализуется циклический сдвиг байтов.

Источник

AES-128. Детали и реализация на python

Идея написать для себя что-то шифрующее родилась довольно тривиально — пришлось завести еще одну дебетовую карту и, следовательно, хранить в голове еще один пин-код. Хранить такую информацию в открытом виде паранойя не позволяет, использовать сторонние сервисы тоже, поэтому после некоторых поисков остановился на стандарте AES. Сразу захотелось разобраться и реализовать алгоритм самому, не прибегая к дополнительным модулям.

В статье я расскажу подробно о составляющих алгоритма, немного окунемся в мат часть и приведу пример реализации на python. В разработке я ограничивался только тем, что входит в состав стандартной библиотеки.

Немного введения

Advanced Encryption Standard является общеизвестным названием алгоритма Rijndael ([rɛindaːl]), который был разработан двумя бельгийскими криптографами Йоаном Дайменом и Винсентом Рэйменом. Алгоритм является блочным и симметричным. Принят в качестве стандарта шифрования данных для гос учреждений в США. Нашумевшее в последнее время Агенство Национальной Безопасности использует его для хранения документов: вплоть до уровня SECRET применяется шифрование с ключом длиной в 128 бит, информация TOP SECRET требует ключа в 192 или 256 бит. В дополнение к высокой криптостойкости алгоритм базируется на не самой сложной математике.

Много шифрования

Для работы нам необходим набор байтов в качестве объекта шифрования и секретный ключ, который потребуется при расшифровке. Длинные ключи хранить в голове неудобно, да и считается, что длины ключа в 128 бит, с лихвой хватает для неприступности, поэтому на варианты 192/256 я не смотрел. К тому же, как сказано здесь, при некоторых условиях более длинный ключ может отставать в устойчивости.

Алгоритм оперирует байтами, считая их элементами конечного поля или поля Галуа GF(2 8 ). Число в скобках — это количество элементов поля или его мощность. Элементами поля GF(2 8 ) являются многочлены степени не более 7, которые могут быть заданы строкой своих коэффициентов. Байт очень легко представить в виде многочлена. Например, байту <1,1,1,0,0,0,1,1>соответствует элемент поля 1x 7 + 1x 6 + 1x 5 + 0x 4 + 0x 3 + 0x 2 + 1x 1 + 1x 0 = 1x 7 + 1x 6 + 1x 5 + x +1. То, что мы работаем с элементами поля, очень важно потому, что это меняет правила операций сложения и умножения. Этого мы коснемся немного позже.

Далее рассмотрим подробно каждую из трансформаций.

SybButes()

Преобразование представляет собой замену каждого байта из State на соответствующий ему из константной таблицы Sbox. Значения элементов Sbox представлены в шестнадцатеричной системе счисления. Сама же таблица получена посредством преобразований уже известного нам поля GF(2 8 )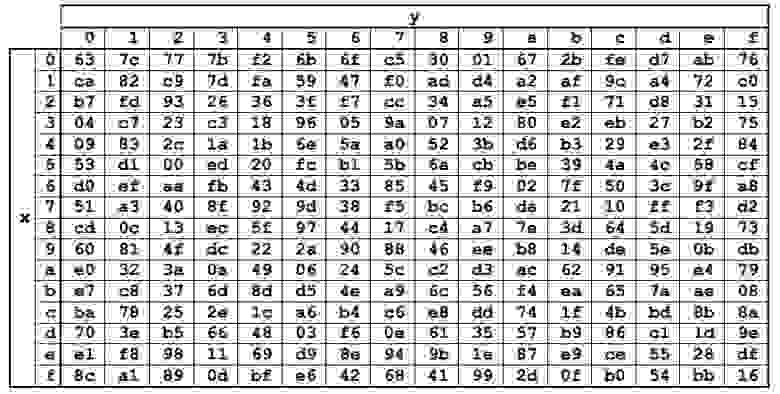

Каждый байт из State можно представить как в шестнадцатеричной системе счисления. Тогда следует заменять его на элемент, стоящий на пересечении строки x и столбца y. Например, <6е>заменится на <9f>, а <15>на <59>.

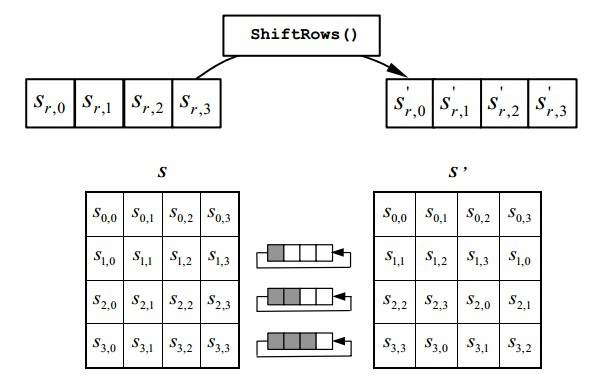
ShiftRows()

Простая трансформация. Она выполняет циклический сдвиг влево на 1 элемент для первой строки, на 2 для второй и на 3 для третьей. Нулевая строка не сдвигается.

MixColumns()

AddRoundKey()

Трансформация производит побитовый XOR каждого элемента из State с соответствующим элементом из RoundKey. RoundKey — массив такого же размера, как и State, который строится для каждого раунда на основе секретного ключа функцией KeyExpansion(), которую и рассмотрим далее.

KeyExpansion()

Эта вспомогательная трансформация формирует набор раундовых ключей — KeySchedule. KeySchedule представляет собой длинную таблицу, состоящую из Nb*(Nr + 1) столбцов или (Nr + 1) блоков, каждый из которых равен по размеру State. Первый раундовый ключ заполняется на основе секретного ключа, который вы придумаете, по формуле
KeySchedule[r][c] = SecretKey[r + 4c], r = 0,1. 4; c = 0,1..Nk.

Понятно, что в KeySchedule мы должны заносить байты, чтобы были возможны дальнейшие операции. Если использовать этот алгоритм для домашнего шифрования, то хранить в голове последовательность чисел совсем не уютно, так что в нашей реализации KeyExpansion() будет на вход брать plaintext строку и применяя ord() для каждого из символов, записывать результат в ячейки KeySchedule. Отсюда вытекают ограничения: не более 16 символов длиной и, так как мы работаем с байтами, ord() символа не должен возвращать значения большие чем 255 или 11111111 в двоичной, иначе получим на выходе неверное шифрование. Получается, что с помощью ключа на русском языке зашифровать не получится.

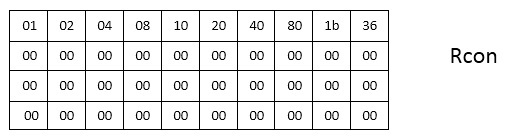
На рисунке изображен макет KeySchedule для AES-128: 11 блоков по 4 колонки. Для других вариаций алгоритма будет соответственно (Nr + 1) блоков по Nb колонок. Теперь нам предстоит заполнить пустые места. Для преобразований опять определена константная таблица — Rcon — значения которой в шестнадцатеричной системе счисления.

Как было сказано ранее, KeySchedule используется в трансформации AddRoundKey(). В раунде инициализации раундовым ключом будут колонки с номерами 0. 3, в первом — с номерами 4. 7 и тд. Вся суть AddRoundKey() — произвести XOR State и раундового ключа.

Это, собственно, все, что касается процесса шифрования. Выходной массив зашифрованных байтов составляется из State по формуле output[r + 4c] = State[r][c], r = 0,1. 4; c = 0,1..Nb. А тем временем статья затягивается, так что мы сейчас быстро пробежимся по процедуре дешифровки.

Быстро о расшифровке

Идея здесь проста: если с тем же ключевым словом выполнить последовательность трансформаций, инверсных трансформациям шифрования, то получится исходное сообщение. Такими инверсными трансформациями являются InvSubBytes(), InvShiftRows(), InvMixColumns() и AddRoundKey(). Общая схема алгоритма расшифровки: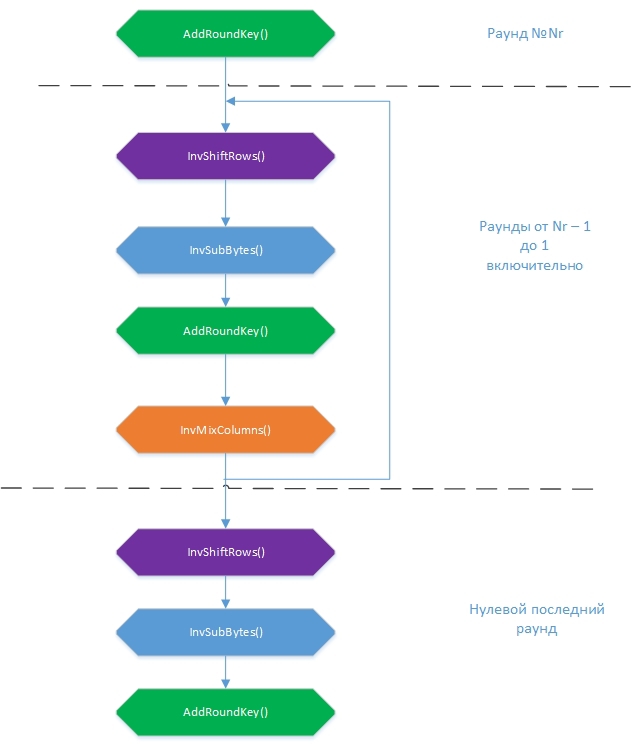

Стоит отметить, что последовательность добавления раундовых ключей в AddRoundKey() должна быть обратной: от Nr + 1 до 0. Изначально, как и при шифровании, из массива входных байтов формируется таблица State. Затем над ней в каждом раунде производятся преобразования, в конце которых должно получиться расшифрованный файл. Порядок трансформаций немного изменился. Что будет первым, InvSubBytes() или InvShiftRows(), на самом деле не важно, потому что одна из них работает со значениями байтов, а вторая переставляет байты, этих самых значений не меняя, но я придерживался последовательности преобразований в псевдокоде стандарта.

InvSubBytes()

InvShiftRows()

InvMixColumns()

AddRoundKey()

Эти две функции на вход берут список байтов, не шифрованных или шифрованных, и plaintext строку с секретным ключевым словом.

Заключение, интересные ссылки

Статья получилась довольно длинной. Я старался разбавлять текст картинками и, надеюсь, вам было интересно и никто не заскучал. Код, представленный в статье, не совсем исчерпывающий. Я не вставлял глобальное объявление константных таблиц, мелких функций для MixColumns(), а только на словах пояснил, что они где-то есть. Не сочтите, что я пиарюсь, но полный, склеенный вместе код можно взять в репозитории. Там же лежит скромный CLI интерфейс, который позволяет просто указать путь до файла, ввести секретный ключ и получить зашифрованный файл в той же директории, что и исходный (расшифрованный файл можно получить таким же способом). Шифруйте на здоровье!

И в конце необходимо сказать об одном немаловажном нюансе — padding или дополнение до блока. AES — алгоритм блочного шифрования, функции encrypt()/decrypt() берут на вход ровно один блок входных байтов (для нашего варианта с ключом в 128 бит это 16 байт). В конце файла могут остаться от 1 до 15 байт, которые не формируют цельный блок. Их можно просто, не шифруя, отдать на запись в конечный файл, но в некоторых случаях, в конце файла может содержаться что-то важное, и такой вариант не подходит. Второй вариант мне подсказала статья на Википедии про блочные шифры

Простое дополнение нулевыми битами не решает проблемы, так как получатель не сможет найти конец полезных данных. К тому же, такой вариант приводит к атакам Оракула дополнения. Поэтому на практике применимо решение, стандартизованное как «Метод дополнения 2» в ISO/IEC 9797-1, добавляющее единичный бит в конец сообщения и заполняющее оставшееся место нулями. В этом случае была доказана стойкость к подобным атакам.

Так я и сделал (хотя первый вариант остался, просто закомментированный. Вдруг и пригодится).

Источник