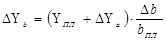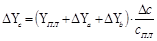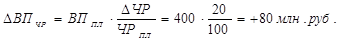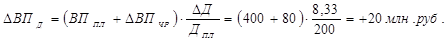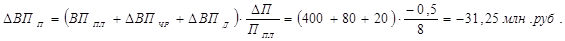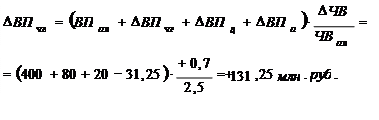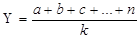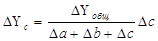Как рассчитывается влияние факторов
Studin.ru
Авторизация
Сейчас на сайте
Взаимопомощь
Теория
Практика
По данным таблицы 1 рассчитать всеми способами влияние факторов на отклонение от плана фактической суммы товарной продукции:
— среднее число дней работы одного рабочего;
— средней продолжительности рабочего дня;
Таблица 1 – Исходные данные
| Показатель | план | факт |
| 1. товарная продукция, тыс. руб. | 982,1 | 936,5 |
| 2. среднесписочная численность работников | 438 | 405 |
| 3. общее количество отработанных всеми рабочими человеко-часов | 795408 | 701460 |
| 3. общее количество отработанных всеми рабочими человеко-дней | 99426 | 89910 |
Решение
Для решения задачи, на основе таблицы 1 рассчитаем необходимые значения факторов
Таблица 2 – Значения факторов
| Показатель | план | факт | Отклонение от плана | Выполнение плана, % |
| среднесписочная численность работников | 438 | 405 | -33 | 92,47 |
| среднее число дней работы одного рабочего | 227 | 222 | -5 | 97,80 |
| средняя продолжительность рабочего дня, часов | 8,00 | 7,80 | -0,20 | 97,52 |
| среднечасовая выработка | 1,23 | 1,34 | 0,10 | 108,13 |
| товарная продукция, руб. | 982100 | 936500 | -45600 | 95,36 |
Рассчитаем влияние данных факторов на отклонение от плана фактической суммы товарной продукции.
1) Способом цепных подстановок.
Зависимость объема товарной продукции от факторов описывается следующей моделью:
где ТП – объем товарной продукцииї;
ЧР – численность рабочих;
Д – среднее число дней работы одного рабочего;
Ч – средняя продолжительность рабочего дня;
В – среднечасовая выработка.
438 · 227 · 8,00 · 1,23 = 982 100 руб.
По цепочке подставляя фактические значения факторов (ЧР1, Д1, Ч1, В1), определим их влияние.
а) Определим влияние численности рабочих:
ΔТПЧР = ТПЧР – ТП0 = 908106,2 – 982100 = – 73993,8 (руб.)
б) Определим влияние среднего количества дней работы одного рабочего:
ΔТПД = ТПД – ТПЧР = 888103,8 – 908106,2 = – 20002,3 (руб.)
в) Определим влияние средней продолжительности рабочего дня:
ΔТПЧ = ТПЧ – ТПД = 866101,3 – 888103,8 = – 22002,6 (руб.)
г) Определим влияние среднечасовой выработки:
ΔТПВ = ТПВ – ТПЧ = 936500 – 866101,3 = 70398,7 (руб.)
2) Способом абсолютных разниц.
Этим методом, влияние факторов определяется по следующими формулами:
а) влияние численности рабочих:
б) влияние среднего количества дней работы одного рабочего:
в) влияние средней продолжительности рабочего дня:
г) влияние среднечасовой выработки:
3) Способом относительных разниц.
Найдем относительное отклонение каждого фактора:
Находим влияние каждого фактора на объем товарной продукции по формулам:
а) влияние численности рабочих:
ΔТПЧР = ТП0 · ΔЧР = 982100 · (– 0,0753) = – 73993,8 (руб.)
б) влияние среднего количества дней работы одного рабочего:
ΔТПД = (ТП0 + ΔТПЧР) · ΔД = (982100 – 73993,8) · (– 0,0220) = – 20002,3 (руб.)
в) влияние средней продолжительности рабочего дня:
г) влияние среднечасовой выработки:
Итак, фактическая сумма товарной продукции по сравнению с планом уменьшилась:
— на 73993,8 руб. – вследствие уменьшения численности рабочих на 33 человека;
— на 20002,3 руб. – вследствие уменьшения среднего количества дней работы одного рабочего на 5 дней;
— на 22002,6 руб. – вследствие уменьшения средней продолжительности рабочего дня на 0,2 часа.
Фактическая сумма товарной продукции увеличилась по сравнению с планом на 70398,7 руб. вследствие роста среднечасовой выработки на 0,10 руб.
Общее влияние четырех факторов:
ΔТПЧР + ΔТПД + ΔТПЧ + ΔТПВ = – 73993,8 – 20002,3 – 22002,6 + 70398,7 = – 45600 руб.
Расчёт влияния факторов способом цепной подстановки
Способ цепной подстановки носит универсальный характер, подходит для всех типов моделей. Позволяет определить влияние отдельных факторов на величину результативного показателя путём постепенной замены базисной величины каждого факторного показателя в объёме результативного показателя на фактическую в данном периоде.
С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трёх и т.д. факторов, допуская, что остальные не меняются.
Количество условных показателей всегда на единицу меньше, чем число факторов модели.
Для четырёхфакторной модели схематически это выглядит таким образом.
| Величина результативного показателя | Условия расчёта результативного показателя | |||
| Фактор1 | Фактор2 | Фактор3 | Фактор4 | |
| По плану | план | план | план | план |
| Условный1 | факт | план | план | план |
| Условный2 | факт | факт | план | план |
| Условный3 | факт | факт | факт | план |
| Фактически | факт | факт | факт | факт |
Используя метод цепной подстановки, необходимо придерживаться следующей последовательности расчётов:
1. В первую очередь учитывается изменение количественных, а затем качественных показателей.
2. Из нескольких количественных или качественных показателей сначала изменяется величина факторов первого уровня подчинения, а потом более низкого.
Пример 16 (согласно схеме):
1. ВП=ЧР×ГВ – двухфакторная модель, рассчитывается один условный показатель.
2. ВП = ЧР × Д × П × ЧВ – четырёхфакторная модель, рассчитываются три условных показателя.
| Показатель | Условное обозначение | Уровень показателя | Отклонение от плана | ||
| план | факт | Абсолютное | Относительное,% | ||
| Валовая продукция, млн. руб. | ВП | ||||
| Среднесписочная численность, чел. | ЧР | ||||
| Среднегодовая выработка продукции 1 рабочим, млн. руб. | ГВ | ||||
| Количество отработанных дней одним рабочим за год | Д | 208,3 | 8,3 | 4,2 | |
| Средняя продолжительность рабочей смены | П | 7,5 | -0,5 | -6,3 | |
| Среднечасовая выработка 1 рабочего, тыс. руб. | ЧВ | 2,5 | 3,2 | 0,7 | 28,0 |
1) Рассчитаем выпуск продукции условный первый (при условии изменения по сравнению с планом только численности рабочих).
ВП усл1 = ЧРф×Дпл×Ппл×ЧВпл=120×200×8×2,5=480 000 тыс. руб.
Изменение выпуска продукции за счёт роста численности рабочих:
∆ ВП (ЧР) = ВП усл1 – ВПпл = 480 000-400 000=80 000 руб.
2) Рассчитаем выпуск продукции условный второй (при условии изменения по сравнению с планом не только численности рабочих, но и количества рабочих дней ).
ВП усл2 = ЧРф×Дф×Ппл×ЧВ пл=120×208,3×8×2,5=499 920 тыс. руб.
Изменение выпуска продукции за счёт увеличения количества рабочих дней в году:
∆ ВП (Д) = ВП усл2-Впусл1= 499920-480 000=19920 руб.
3) Рассчитаем выпуск продукции условный третий (при условии изменения по сравнению с планом не только численности рабочих и количества рабочих дней, но и продолжительности рабочей смены ).
ВП усл3 = ЧРф×Дф×Пф×ЧВпл=120×208,3×7,5×2,5=468 675 тыс. руб.
Изменение выпуска продукции за счёт сокращения средней продолжительности смены:
4) Изменение выпуска продукции за счёт увеличения часовой выработки (производительности труда):
∆ ВП (ЧВ) = ВПф – Вп усл3= 600 000 – 468675= 131 325 тыс. руб.
Проверка правильности расчётов (сумма факторов должна быть равна абсолютному отклонению фактической величины выпуска продукции от плана):
80 000 + 19 920 – 31 245 + 131 325 = 200 000
Вывод: Перевыполнение плана по выпуску продукции обусловлено, в первую очередь, ростом производительности труда (на 131 325 тыс. руб.), во вторую очередь – созданием дополнительных рабочих мест (на 80 000 тыс. руб.), а так же введением дополнительных рабочих дней (на 19 920 руб.). Потери товарной продукции в размере 31 325 тыс. рублей связаны с внутрисменными простоями производства.
Расчёт влияния факторов способом абсолютных разниц в АХД.
Этот способ значительно проще в применении, чем предыдущий, но применяется только в мультипликативных и мультипликативно-аддитивных моделях. А, кроме того, даёт несколько большую погрешность в вычислениях.
Величина влияния факторов на результативный показатель рассчитывается
умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, которые находятся слева от него в модели.
Алгоритм расчёта для модели выпуска валовой продукции будет выглядеть следующим образом:
ВП=ЧР×Д×П×ЧВ
∆ ВП(ЧР)= ∆ЧР×Дпл×Ппл×ЧВпл
∆ВП(Д) = ЧРф×∆Д×Ппл×ЧВпл
∆ ВП (П)=ЧРф×Дф×∆П×ЧВпл
∆ ВП(ЧВ)=ЧРф×Дф×Ппл×∆ЧВ
Результаты применения такие же, как при методе цепной подстановки. Алгебраическая сумма прироста результативного показателя за счёт отдельных факторов должна быть равна его общему приросту.
Расчёт влияния факторов на выпуск продукции по данным, приведённым в примере на стр. 12, будет выглядеть следующим образом.
∆ ВП(ЧР)=20×200×8×2,5=80 000 тыс. руб. – рост выпуска продукции за счёт увеличения численности рабочих
∆ВП(Д)= 120×8,3×8×2,5=19 920 тыс. рублей – рост выпуска продукции за счёт введения дополнительных рабочих дней в году
∆ ВП (П)= 120×208,3×(-0,5)×2,5= – 31245 тыс. руб. – снижение выпуска продукции за счёт внутрисменных простоев
∆ ВП(ЧВ)= 120×208,3×7,5×0,7=131 229 тыс. руб. – рост выпуска продукции за счёт увеличения часовой выработки (производительности труда).
Примечание. Метод абсолютных разниц даёт меньшую точность вычислений, по сравнению с методом цепной подстановки.
Например, ∆ ВП(ЧВ)= 131 229 тыс. руб., а не 131 325 тыс. руб. (согласно метода цепной подстановки). Следует иметь в виду, что чем точнее округление всех численных величин факторов (желательно хотя бы до двух знаков после запятой), тем точнее будут расчёты.
ЗАДАНИЕ ДЛЯ САМОКОНТРОЛЯ
1. Балансовый метод в АХД заключается:
1) в сопоставлении разнородных экономических величин,
2) в сопоставлении однородных экономических величин,
3) в делении экономической информации на группы,
4) в сопоставлении заведомо тождественных итогов экономических расчётов.
2. Для приведения в сопоставимый вид (в целях сравнения) величин объёмов выпуска однородной продукции, различающиеся по уровню качества, используют:
1) индекс изменения объёмов производства,
2) стандартные нормы качества продукции,
3) индекс роста цен (инфляции),
4) показатель себестоимости единицы продукции.
3. Для приведения в сопоставимый вид показателей себестоимости объёмов выпуска товарной продукции используют:
1) стандартные нормы качества продукции,
2) индекс роста цен (инфляции),
3) показатель себестоимости единицы продукции.
4. Деление предприятий на группы по степени фондовооружённости в целях выявления взаимосвязи между фондовооруженностью труда и производительностью труда является примером:
1) структурной группировки,
2) типологической группировки;
3) аналитической группировки,
5. Деление предприятий на группы по отраслям является примером группировки:
Определите, верно ли по Вашему мнению данное утверждение: «Факторы в модели факторного анализа располагаются слева направо в порядке возрастания значимости».
Определите, верно ли по Вашему мнению данное утверждение: «Способ абсолютных разниц, применяемый при факторном анализе, является универсальным и может использоваться для любых видов моделей (уравнений)».
8. Применение способа абсолютных разниц при факторном анализе предполагает расчёт:
1) абсолютных отклонений,
2) относительных отклонений,
3) ряда условных величин исследуемого результативного показателя,
Факторный анализ: оцениваем причины изменения показателей
Факторный анализ: оцениваем причины изменения показателей
Кандидат экономических наук, доцент. Автор двух монографий, шести учебных пособий и нескольких десятков статей по вопросам бухгалтерского учета, финансового менеджмента и анализа. Лауреат премии губернатора в сфере науки, техники и инновационной деятельности за 2012 г. За плечами — опыт работы главбухом бюджетного учреждения и преподавателем государственного вуза.
Факторный анализ: что это и зачем нужен
Факторный анализ – это оценка влияния одних показателей на другие. Например, вы хотите узнать причину снижения финансового результата. Для этого нужно посчитать, какое воздействие на него оказали доходы и расходы. Или вам важно понять, почему просела рентабельность собственного капитала. Тогда исследуйте, какой вклад в процесс внесли прибыль на рубль активов и структура пассивов.
Предлагаем скачать Excel-файл. В него встроили четыре формулы для анализа рентабельности активов, продукции и собственного капитала.
Вот три вопроса, ответы на которые понадобятся, чтобы провести подобные расчеты.
Первый. Что такое факторная модель.
Это формульная взаимосвязь между основным показателем, который вы анализируете, и теми, что на него влияют.
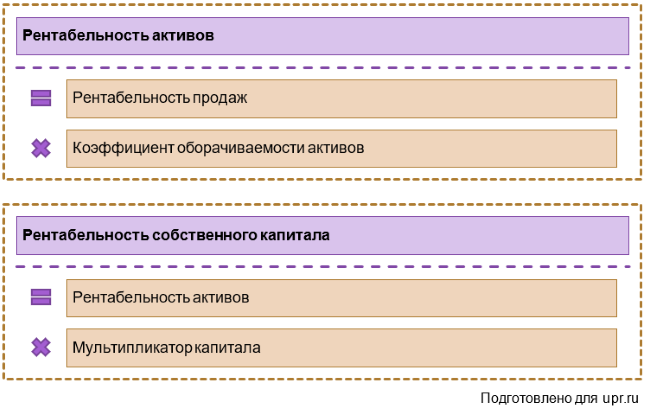
Откуда ее взять? Есть готовые варианты. К примеру, факторные модели DuPont для рентабельности активов и собственного капитала. Вот они:
Рисунок 1. Факторные модели DuPont для рентабельности активов и собственного капитала
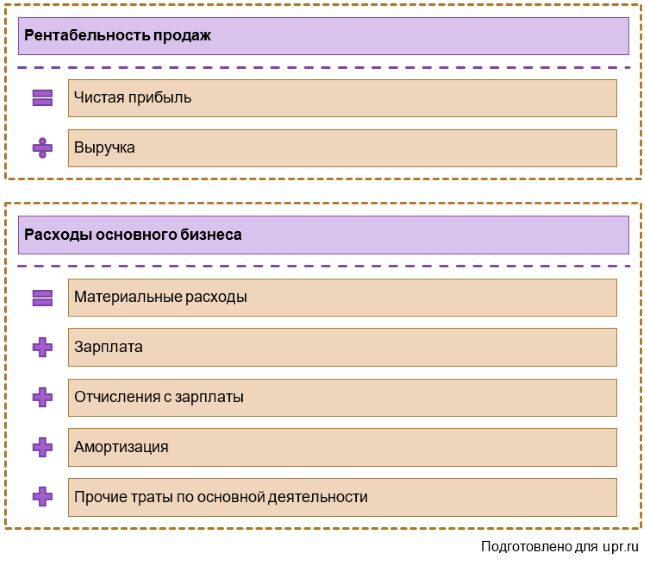
Можно составить зависимость самим. Иногда это несложно. Особенно, если отталкиваться от базовой формулы расчета показателя. Приведем два простых примера, основанных на таком подходе:
Рисунок 2. Примеры факторный моделей
Условимся называть искомое значение в формулах «результатом», а прочие показатели «факторами».
Второй. Почему иногда универсальной зависимости между результатом и факторами нет.
Потому что есть два типа факторного анализа:
Примеры, которые привели выше, относятся к первому варианту. Их особенность в том, что взаимосвязь между показателями однозначна и работает для любой организации. Допустим, чистая прибыль выросла в два раза при неизменном значении выручки. Значит, рентабельность продаж тоже увеличится в два раза. По-другому не бывает.
Стохастический вариант предполагает: зависимость между результатом и факторами есть, но одинаково определить ее для всех компаний не получится. Например, индексация зарплаты способна поднять производительность труда работников. Но как соотносятся проценты повышения? Если заложим в расходы двукратный рост оплаты труда, то на сколько именно увеличится людская отдача? Для каждой организации ответ свой. Более того, он свой даже для одного и того же предприятия, но в разные месяцы и годы.
Чтобы не усложнять, далее в статье все сведем только к детерминированным зависимостям.
Третий. Как посчитать влияние факторов на результат.
Для этого есть специальные методы. К примеру, метод цепных подстановок, абсолютных и относительных разниц. Это не полный перечень. Но знать все необязательно. В следующих частях материала расскажем теорию про два основных подхода и покажем примеры использования.
Модели и методы факторного анализа
Начнем с видов моделей. Они – это форма взаимосвязи между факторами. Выше приводили примеры, где показатели складывались, перемножались или делились один на другой. Это и определяет вид. Смотрите на схеме четыре возможных варианта.
Теперь расскажем про методы. То есть про то, как посчитать влияние факторных показателей на результирующий. Остановимся на двух подходах:
Первый вариант хорош своей универсальностью. Подойдет для модели любого типа.
Второй отличается чуть большей простотой вычислений, однако используется с ограничениями. Пригодится, когда анализируете мультипликативные модели или смешанные мультипликативно-аддитивные.
Схема действий для цепных подстановок такая:
Вот как это выглядит на практике:
Немного пояснений к схеме:
Но для них выше сложность реализации.
А вот этапы для способа абсолютных разниц:
Чтобы было понятнее, подготовили схему.
Согласитесь, этот подход проще, чем цепные подстановки. Все бы с ним хорошо, если бы не упомянутое выше ограничение в применении по типам моделей.
Хотя запутаться в подобных расчетах негде, однако есть смысл сделать проверку. Сложите все факторные влияния и сравните полученное с абсолютным изменением результата за период. Если сходится, значит, все правильно.
Как провести факторный анализ: пример
Теперь закрепим написанное расчетами для реальной компании. Понадобится ее финансовая отчетность. А еще нужно определиться с моделями.
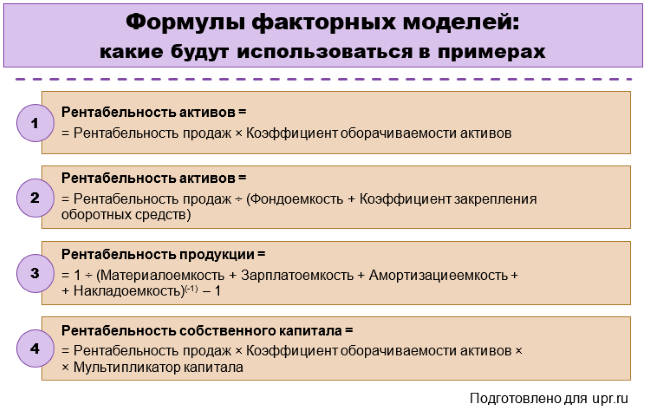
Будем основываться на цифрах из баланса и отчета о финансовых результатах за 2021 г. для ПАО «КАМАЗ». Воспользуемся четырьмя факторными моделями. Их формулы показали на схеме. Первая и последняя – это простая и расширенная формулы DuPont.
Анализируем рентабельность активов по двухфакторной модели
Исходные данные и расчетные значения свели в таблицу. Так как модель мультипликативная, то применили способ абсолютных разниц.
Показатель, млн руб. (если не указано иное)
– активы на начало года
– активы на конец года
– чистая прибыль (убыток)
– рентабельность (убыточность) активов (Ра), %
– рентабельность (убыточность) продаж (Рп), %
– коэффициент оборачиваемости активов (Коа), ед.
Факторное влияние на рентабельность активов, %:
Суммарное влияние факторов 1,61 соответствует абсолютному изменению рентабельности активов за 2019-2020 гг. Значит, ошибки в расчетах нет. Есть смысл перейти к анализу цифр. Вот краткие выводы:
Анализ по первой модели рассказал о трех особенностях функционирования компании:
Оцениваем рентабельность активов по трехфакторной модели
По проведенным расчетам заметили: доходная отдача от активов у ПАО «КАМАЗ» не столь велика. Посмотрим, какая их составляющая «проседает» в этом отношении особенно сильно. Поможет трехфакторная модель. Цифры по ней находятся в таблице. Для определения факторного влияния применили способ цепных подстановок, так как абсолютные разницы для модели данного смешанного типа не подходят.
Показатель, млн руб. (если не указано иное)
– внеоборотные активы на начало года
– внеоборотные активы на конец года
– оборотные активы на начало года
– оборотные активы на конец года
– рентабельность (убыточность) активов (Ра), %
– рентабельность (убыточность) продаж (Рп), %
– фондоемкость (Фе), руб./руб.
– коэффициент закрепления оборотных средств (Кз), руб./руб.
Факторное влияние на рентабельность активов, %:
– коэффициента закрепления оборотных средств
∆Ра = ∆Ра(Рп) + ∆Ра(Фе) + ∆Ра(Кз)
Знаки влияния фондоемкости и закрепления оборотных средств показывают, какая именно часть активов в 2020-м использовалась менее эффективно. Минус у Фе говорит, что это внеоборотные активы. Почему так? Потому что их стоимостное увеличение обогнало прирост выручки. Выходит, чтобы заработать 1 руб. дохода от основной деятельности в 2020-м требовалось больше зданий, оборудования, транспорта и т.п.
В отношении оборотных активов ситуация иная: они тоже увеличились, но выручка приросла значительнее. Выходит, отдача с каждого вложенного в них рубля стала больше.
Мы показываем пример общего анализа, поэтому на частностях не останавливаемся. В реальной же практике они должны быть. Например, разумно посмотреть, какие именно составляющие внеоборотных активов стали использоваться менее эффективно. Для этого рассчитываются значения фондоемкости по отдельным составляющим долгосрочного имущества. Затем принимается решение: насколько разумно сохранять и приумножать объемы подобных активов, если отдача от них падает и тормозит рост бизнеса.
Ответ на такой вопрос нельзя предсказать заранее. В каждой конкретной ситуации он будет свой. К примеру, у ПАО «КАМАЗ» в 2020-м значительно увеличились долгосрочные финансовые вложения. Это предоставленные займы на срок свыше года и участие в уставных капиталах других компаний. Они тоже относятся к внеоборотным активам. Если предприятие планирует получать от них стабильный, причем существенный доход, то их рост оправдан.
Аналогичное мнение относительно суммы вложений в имущество и ожидаемой от него доходности разумно сформулировать по каждому значимому элементу первого раздела баланса.
Выявляем влияние факторов на рентабельность продукции
Данная модель поможет понять структуру себестоимости. А еще, какой ее элемент растет скорее остальных, а потому особенно сильно «съедает» прибыль бизнеса. Расчеты привели в таблице. Влияние факторов оценивали цепными подстановками.
Показатель, млн руб. (если не указано иное)
Тема 3. Способы измерения влияния факторов в анализе хозяйственной деятельности



Способ цепной подстановки
Определение величины влияния отдельных факторов на прирост результативных показателей является одной из методологических задач в АХД. В детерминированном анализе для этого используются следующие способы: цепной подстановки, абсолютных разниц, относительных разниц, пропорционального деления, интегральный, логарифмирования, балансовый и др.
Наиболее универсальным из них является способ цепной подстановки. Сущность способа состоит в применении подстановок: последовательной замене базисных (плановых) величин каждого фактора фактическими, причем каждый раз заменяется одна из величин, а остальные закрепляются на определенном уровне. С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и последующих факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминировать влияние всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Если требуется определить влияние четырех факторов, то в этом случае рассчитывается три условных показателя, т.е. количество условных величин результативного показателя на единицу меньше числа факторов.
Проиллюстрируем это на четырехфакторной модели валовой продукции:
Исходные данные для решения задачи приведены в таблице 3.1.
Данные для факторного анализа объема валовой продукции
| Показатель | Условное обозначение | Уровень показателя | Отклонение от плана | ||
| план | факт | абсолютное | относительное, % | ||
| Валовая продукция, млн. руб. | ВП | + 150 | +50 | ||
| Среднесписочная численность рабочих | ЧР | +20 | +20 | ||
| Среднегодовая выработка продукции одним рабочим, млн. руб. | ГВ | +1 | +25 | ||
| Количество отработанных дней одним рабочим за год | Д | 208,3 | +8,3 | +4,17 | |
| Среднедневная выработка рабочего, тыс. руб. | ДВ | +4 | +20 | ||
| Средняя продолжительность смены, ч | П | 7,5 | -0,5 | -5 | |
| Среднечасовая выработка продукции одним рабочим, тыс. руб. | ЧВ | 2,5 | 3,2 | +0,7 | +28 |
План по выпуску продукции в целом перевыполнен на 200 млн. руб. (600-400), в том числе за счет изменения:
1) Количества рабочих
2) Количества отработанных дней одним рабочим за год
3) Средней продолжительности рабочего дня
4) Среднечасовой выработки
Используя способ цепной подстановки, необходимо придерживаться следующей последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки.
Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Способ абсолютных разниц
Способ абсолютных разниц применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях 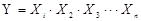
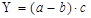
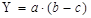
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста значения исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Алгоритм расчета для мультипликативной четырехфакторной модели валовой продукции выглядит следующим образом:
Таким образом, с помощью способа абсолютных разниц получаются те же результаты, что и способом цепной подстановки.
Способ относительных разниц
Способ относительных разниц применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях. Здесь используются относительные приросты факторных показателей, выраженные в виде коэффициентов или процентов. Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа 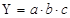
Изменение результативного показателя определяется следующим образом:
Согласно этому правилу для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в виде десятичной дроби.
Чтобы рассчитать влияние второго фактора, нужно к плановой (базисной) величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора.
Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.
Закрепим рассмотренную методику на примере, приведенном в табл. 3.1:
Как видим, результаты расчетов такие же, как и при использовании предыдущих способов.
Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитывать влияние большого комплекса факторов (8-10 и более). В отличие от от предыдущих способов здесь значительно сокращается число вычислительных процедур, что обуславливает его преимущество.
Способ пропорционального деления и долевого участия
В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями Y=Σxì. и моделями кратно-аддитивного типа:
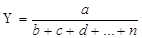
В первом случае, когда имеем одноуровневую модель типа Y=a+b+c, расчет проводится следующим образом:
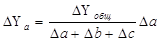
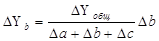
В моделях кратно-аддитивного вида сначала необходимо способом цепной подстановки определить, насколько изменился результативный показатель за счет числителя и знаменателя, а затем произвести расчет влияния факторов второго порядка способом пропорционального деления по вышеприведенным алгоритмам.
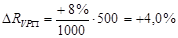
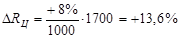
Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя (табл. 3.2.):
Расчет влияния факторов на результативный показатель способом долевого участия
Кроме данных способов измерения влияния факторов в анализе хозяйственной деятельности существует и ряд других, таких как использование интегральный метод в АХД, приемы корреляционного анализа.