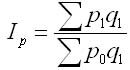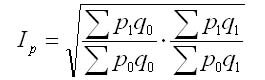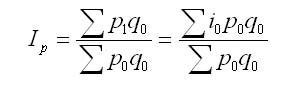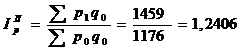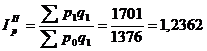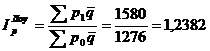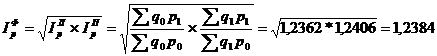Как рассчитывается индекс ласпейреса
Индекс цен, индекс Пааше, индекс Ласпейреса, индекс Фишера
В условиях современной экономики и эконометрике важное место среди индексов качественных показателей отвелось индексу цен, который представляет собой показатели динамики уровня цен.
При помощи индекса потребительских цен (ИПЦ) проводится оценка динамики цен на товары производственного и непроизводственного потребления. ИПЦ отражает динамику ценконечного потребления, измеряет общее изменение стоимости фиксированного набора потребительских товаров и услуг («потребительская корзина»), а также является одним из основных показателей, характеризующих уровень инфляции. ИПЦ используется при корректировке минимального размера труда, расчета ставок налогов и т. д.
Индекс Пааше
В 1874 г. немецкий экономист Г. Пааше предложил агрегатный индекс цен с отчетными весами. Формула агрегатного индекса цен Пааше определяется так:
Где числитель — фактическая стоимость продукции отчетного периода;
Знаменатель — условная стоимость товаров, которые реализованы в отчетном периоде по базисным ценам.
Индекс цен Пааше показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом, т. е. он показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.
В 1864 г. немецкий экономист Э. Ласпейрес предложил индекс, отражающий изменение цен и строится по продукции базисного периода.
Индекс Ласпейреса
Формула агрегатного индекса цен Ласпейреса рассчитывается как отношение:
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по продукции, которая была реализована в базисном периоде, и экономию (перерасход), который можно было бы получить от изменения цен. Индекс цен Ласпейреса также показывает, во сколько раз товары базисного периода подорожали (подешевели) в результате изменения цен на них в отчетном периоде.
Индекс Фишера
Американский экономист И. Фишер предложил «идеальный» индекс цен, который назвали его именем, представляющий собой среднюю геометрическую произведения двух агрегатных индексов цен Ласпейреса и Пааше.
Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т. е. при перестановке базисного и отчетного периодов полученный обратный индекс представляет собой величину, обратную величине первоначального индекса. Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).
Средний гармонический индекс цен
Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.
Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным.
Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:
Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.
Средний арифметический индекс цен
Средний арифметический индекс цен получают в том случае, если из индивидуального индекса цен ip = p1/p0 выразить цену отчетного периода p1 = i0p0, а затем подставить ее в числитель агрегатного индекса цен.
Данный индекс аналогичен агрегатному индексу Ласпейреса и имеет формулу:
В этом индексе весами осредненных индивидуальных индексов служит объем товарооборота в базисном периоде.
Расчет индекса цен: примеры, формулы, онлайн-калькулятор
Быстрая навигация по странице:
Система индексов цен
Контроль цен имеет важное значение в экономике. Комплекс показателей статистики цен состоит их широкого спектра критериев, позволяющих изучить различные аспекты величины, изменения и структуры стоимости товаров и услуг. В процессе исследования изучаются розничные цены и тарифы, оптовые, отпускные, закупочные, сметные, мировые и другие виды цен. Одним из важнейших инструментов такого анализа выступают различные индексы цен: Ласпейреса и Пааше, агрегатные и средние из индивидуальных, Фишера и т.п. Изменение средних цен исследуется посредством системы следующих индексов: переменного состава, постоянного состава и структурных сдвигов (данные показатели взаимосвязаны). В целом рассчитываемые показатели являются относительными, которые отражают соотношение уровней какого-либо явления во времени или в пространстве и позволяет выполнить сравнение фактических значений с эталонными, плановыми, прогнозными и т.п. величинами. По степени охвата рассматриваемые показатели могут быть как индивидуальными (при расчете, например, для конкретного товара), так и сводными (при расчете значений, например, по группе товаров). По базе сравнения рассматриваемые показатели относятся к динамическим (например, при анализе изменения стоимости набора продуктов питания за различные периоды времени), но могут рассчитываться и территориальные значения. По форме построения рассматриваемые показатели могут быть как агрегатными, так и средними.
Размещено на www.rnz.ru
Формула индекса цен
В зависимости от вида индекса можно использовать несколько формул, позволяющих вычислить индекс цен. Так, при расчете индивидуальных индексов используют следующую формулу:

Для расчета значения сводного (общего, агрегатного) индекса цен применяется формула Пааше:

В силу специфики правового регулирования индекс потребительских цен в РФ рассчитывается на основе формулы Ласпейреса (Ласпейраса):

Модифицированная формула, применяемая для практических вычислений при проведении статистического наблюдения, приводится в Приказе Росстата от 30.12.2014 N 734 «Об утверждении Официальной статистической методологии организации статистического наблюдения за потребительскими ценами на товары и услуги и расчета индексов потребительских цен».
Пример расчета индекса цен
Исходные данные: имеется следующая информация о реализации товаров предприятиями города:
| Продукция | Базисный период | Отчетный период | ||
|---|---|---|---|---|
| Стоимость единицы, руб. | Количество, шт. | Стоимость единицы, руб. | Количество, шт. | |
| Товар №1 | 25 | 15 | 22 | 17 |
| Товар №2 | 18 | 24 | 19 | 25 |
| Товар №3 | 16 | 45 | 18 | 44 |
На основе исходных данных определить индивидуальные и общий индекс цен, индекс потребительских цен, потери покупателей от роста цен (или экономию в случае их снижения).
Составим таблицу вспомогательных расчетов:
Вычислим индивидуальные индексы цен:
Общий (агрегатный) индекс цен рассчитаем по формуле Пааше:
Индекс потребительских цен рассчитаем по формуле Ласпейреса:
Ip = ∑p1q0 : ∑p0q0 = 1596 / 1527 = 1,045. Полученное значение индекса показывает, что уровень потребительской инфляции по рассматриваемой группе товаров составил 4,5%.
Онлайн калькулятор индекса цен
Для вычисления агрегатного индекса цен и индекса потребительских цен приводим простую форму онлайн-калькулятора, используя который, Вы можете самостоятельно выполнить расчет данных показателей и заполнить таблицу. Для получения правильных результатов работы онлайн-калькулятора в процессе ввода данных необходимо внимательно соблюдать размерность полей, что позволит выполнить необходимые вычисления быстро и точно. Дробные величины должны вводиться с ТОЧКОЙ, а не с запятой! В представленной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает расчет индекса потребительских цен онлайн. Для вычисления указанных показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет».
Индекс цен Пааше и Ласпейреса
Существует два способа расчета индексов цен: индексы цен Пааше и Лайспейреса.
Индекс цен Ласпейреса
— стоимость продукции реализованной в базисном (предыдущем) периоде по ценам отчетного периода
— фактическая стоимость продукции в базисном периоде
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но на товары реализованные в базисном периоде. Иначе говоря индекс цен Ласпейреса показывает во сколько товары базисного периода подорожали или подешевели из-за изменения цен в отчетном периоде.
Индекс цен Пааше
Индекс цен Пааше — это агрегатный индекс цен с весами (количество реализованного товара) в отчетном периоде.
— фактическая стоимость продукции отчетного периода
— стоимость товаров реализованных в отчетном периоде по ценам базисного периода
Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде. То есть индекс цен Пааше показывает на сколько подешевели или подорожали товары.
Значения индексов цена Пааше и Ласпейреса для одних и тех же данных не совпадают, так как имеют разное экономическое содержание и следовательно применяются в разных ситуациях.
В отечественной статистике до перехода к рыночным отношениям отдавали предпочтение индексу цен Пааше. Но из-за особенностей расчета начиная с 1991 года вычисление общего уровня цен на товары и услуги начали проводить по формуле Ласпейреса. Связано это с тем что во время инфляции или экономических кризисов многие товары могут выпасть из потребления. При исчислении по формуле Пааше не учитываются товары спрос на которые упал, поэтому при исчислении индекса цен по формуле Пааше небходим частый перерасчет информации для формировании правильной системы весов. В связи с этим и в международной практике прибегли к расчету индексов цен по формуле Ласпейреса.
Идеальный индекс цен Фишера
Представляет собой среднюю геометрическую из произведений двух агрегатных индексов цен Ласпейреса и Пааше:
Идеальность заключается в том, что индекс является обратимым во времени, то есть при перестановке базисного и отчетного периодов получается обратный индекс (величина обратная величине первоначального индекса).
Индекс цен Фишера лишен какого-либо экономического содержания. В силу сложности расчета и трудности экономической интерпретации ипользуется довольно редко (например при исчислении индексов цен за длительный период времени для сглаживания значительных изменений).
Индексы цен Ласпейреса, Пааше, Фишера, Лоу



Индексы цен, рассчитанные по формуле Ласпейреса, особенно широко применяются при расчете индексов потребительских цен (ИПЦ), индексов цен производителей на промышленную продукцию по данным о ценах на товары-представители. Однако данный индекс не включает инвестиционные товары, но при этом учитываются цены на импортную продукцию.
Индексы цен, рассчитанные по формуле Пааше, как правило, охватывают более широкий круг товаров и услуг. В качестве весов используется не структура потребительских расходов, а структура товарооборота, или добавленной стоимости, или произведенной продукции в текущем периоде, поэтому они могут быть определены лишь по истечении отчетного периода. Индекс цен Пааше —это индекс розничных цен, используется при измерении динамики цен компонентов ВВП, закупочных цен в сельском хозяйстве, сметных цен в строительстве, экспортных цен.
Индекс цен Ласпейреса в качестве весов использует физический объем продукции базисного периода:
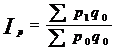
Этот индекс показывает, во сколько бы раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде при неизменной базисной структуре товаров-представителей, вошедших в потребительскую корзину.
Известно, что в индексе цен Ласпейреса весами служит продукция (потребительская корзина) в базисном периоде, и по мере отдаления от базисного года эта потребительская корзина все более, по видам, количеству и качеству вошедших в нее товаров-представителей, претерпевает изменение. Естественно, система весов должна пересматриваться при выборе базисного года, поэтому следует соблюсти критерии:
— базисный год должен находиться в середине длительной фазы подъема (снижения) экономического развития;
— динамика цен в базисном году не должна быть стабильной, но не должна быть и ниже, чем в соседние с ним годы;
— год должен быть «нормальным» с точки зрения различных катаклизмов.
Увязка индекса, рассчитанного по новым весам, осуществляется с помощью процедуры смыкания динамических рядов.
Индексируемой величиной виндексе цен Пааше являются цены, а весами выступает количество продукции отчетного периода.
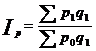
Этот индекс отвечает на вопрос: насколько товары и услуги в отчетном периоде стали дороже (дешевле), чем в базисном периоде?
Значения индексов не совпадают. Отличие значений объясняется тем, что индексы имеют разное экономическое содержание.
Индекс цен Фишера — это корень квадратный из произведения индексов цен Ласпейреса и Пааше. Экономического содержания этот индекс не имеет. Чаще всего он применяется при исчислении индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объема продукции, в которых происходят значительные изменения:
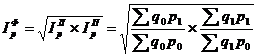
Индекс цен Фишера оценивает не только набор товаров базисного периода по ценам отчетного периода (Σq0р1), но и набор товаров отчетного периода по ценам базисного (Σq1р0). Этот индекс еще называют «идеальным» индексом, так как он является обратимым во времени.
При синтезировании общего индекса цен фактического количества товаров (в отчетный или базисный периоды) в качестве соизмерителей индексируемых величин (р1 и р0) могут применяться средние величины реализации товаров за два или большее периодов. При таком расчете формула общего индекса цен будет выглядеть следующим образом:
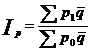
Такой индекс называется индекс Лоу. Если при определении индекса цен исходная информация содержит лишь данные о количестве реализации товаров в базисном и текущем периодах, то средняя их величина определяется: 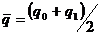
Индекс цен Лоу применяется при расчетах закупок или реализации товара в течении продолжительных периодов времени (пятилетках, десятилетиях и т.д.). Этот метод дает возможность анализа цен с учетом происходящих внутри отдельных субпериодов изменений в ассортиментном составе товаров.
Пример 1:
На основе имеющихся данных оценить изменение цен.
| товар | р0 | q0 | p1 | q1 | p0q0 | p1q1 | p0q1 | p1q0 | q cp | p0q cp | p1q cp |
| а | 15 | 10 | 17 | 15 | 150 | 255 | 225 | 170 | 12,5 | 187,5 | 212,5 |
| б | 10 | 13 | 13 | 18 | 130 | 234 | 180 | 169 | 15,5 | 155 | 201,5 |
| в | 17 | 28 | 20 | 31 | 476 | 620 | 527 | 560 | 29,5 | 501,5 | 590 |
| г | 12 | 35 | 16 | 37 | 420 | 592 | 444 | 560 | 36 | 432 | 576 |
| итого |
Задачи для самостоятельного решения:
Задача 53.
Имеются следующие данные о поставках продукта А:
| Страна-импортер | Объем поставок (тыс. шт.) | Внешнеторговая цена (долл.) | |
| базисный период, | отчетный период, | базисный период, | отчетный период, |
| Болгария | |||
| Германия | |||
| Китай | |||
| Итого | — | — |
Рассчитайте: 1) среднюю цену поставок продуктаА; 2) индексы переменного состава, постоянного состава и структурных сдвигов, характеризующие динамику средней внешнеторговой цены.
Задача 54.
Имеются данные об объемах платных услуг образования и здравоохранения:
| Услуги | Объем платных услуг в текущих ценах, ден. ед. | Изменение цен, % |
| базисный период | отчетный период | |
| 1. Образование | +10 | |
| 2. Здравоохранение в том числе: а) хирургические | +14 | |
| б)терапевтические | +17 | |
| в)другие | +10 |
Сводный индекс цен по полному набору товаров-представителей, исчисленный по формуле цен Ласпейреса, — 0,98. Определите:
1. а) как изменились бы потребительские расходы населения на приобретение платных услуг образования и здравоохранения при неизменной структуре их потребления;
б) какие факторы оказали влияние на это изменение и в какой степени;
в) как изменилась стоимость жизни.
2. Постройте сводный индекс розничных цен на платные услуги образования и здравоохранения.
3. Сделайте выводы по каждому исчисленному показателю.
Задача 55.
Рассчитайте общее и среднее изменение цен на готовую продукцию легкой промышленности, исходя из следующих данных за 8 месяцев текущего года (в % к предыдущему месяцу):
| январь | февраль | март | апрель | май | июнь | июль | Август |
| 103,3 | 102,8 | 94,6 | 99,9 | 94,5 | 101,6 | 100,9 | 106,7 |
Задача 56.
Определите индекс товарооборота; индексы цен Ласпейреса и Пааше, если известно, что за отчетный период цена единицы изделия А выросла на 5%, изделия Б – снизилась на 5%, изделия В – выросла на 11%. Объем товарооборота в отчетном периоде по изделиям А,Б,В соответственно 780, 500, 420 ден.ед., что от товарооборота базисного периода соответственно по товарам А,Б,В составляет 1,06, 0,98, 1,17.
Задача 57.
Имеются следующие данные о реализации товаров:
| Товар | Цены, ден.ед. | Объемы реализации, тыс.шт. |
| А | 5,2 | 25,1 |
| Б | 6,3 | 37,6 |
| В | 4,7 | 23,4 |
| Г | 8,5 | 40,2 |
Рассчитать индексы цен Ласпейреса, Пааше, Лоу. Сделайте выводы.
Задача 58.
Рассчитайте сводные индексы потребительских и розничных цен, исходя из данных по основным товарным группам:
| Товарные группы | Индекс цен за VI 2009 г. к XII 2008 г. | Удельный вес каждой товарной группы по состоянию на: | |
| XII 2008 г. | VI 2009 г. | ||
| Мясо и мясопродукты | 1,58 | 0,3717 | 0,2875 |
| Молоко и молочные продукты | 1,99 | 0,3109 | 0,2769 |
| Рыба и рыбопродукты | 1,89 | 0,0650 | 0,0646 |
| Сахар | 1,08 | 0,1631 | 0,1106 |
| Хлебные продукты | 2,34 | 0,0893 | 0,2604 |
| итого | 1,0000 | 1,0000 |
Задача 59.
По нижеследующим данным рассчитайте индексы цен Ласпейреса, Пааше, Фишера. Проанализируйте полученные результаты.
| Базисный период | Отчетный период | ||
| Цена за единицу, ден.ед. | Произведено, шт. | Цена за единицу, ден.ед. | Произведено, шт. |
| А | |||
| Б | |||
| В |
Задача 60.
Производство изделий в натуральном выражении снизилось в 1,2 раза по сравнению с прошлым годом, а стоимость продукции увеличилась в 2 раза. На сколько процентов выросли цены на данные изделия?
Вопросы для подготовки к экзамену по дисциплине «Экономическая статистика»
1. Предмет, методы и задачи экономической статистики
2. Система показателей экономической статистики
3. Общее понятие о классификациях, группировках и номенклатурах
4. Отраслевые классификации
5. Население как объект статистического изучения
6. Изучение численности населения
7. Движения населения. Перспективные расчеты численности населения.
8. Статистика занятости и безработицы
9. Показатели движения рабочей силы
10. Рабочее время. Баланс рабочего времени.
11. Использование рабочего времени.
12. Статистика оплаты труда. Состав фонда заработной платы.
13. Показатели уровня и динамики заработной платы. Дифференциация заработной платы
14. СНС (общие понятия).
15. Основные счета СНС
16. Система макроэкономических показателей. ВВ, ВДС.
17. Методы определения ВВП. Дефлятор ВВП.
18. Исчисление показателей ВВП в постоянных ценах
19. Национальное богатство. Классификация его элементов. Оценка национального богатства страны.
20. Виды оценки и износ основных фондов.
21. Баланс основных фондов. Показатели состояния, движения и использование основных фондов.
22. Структура финансового рынка. Кредитный рынок (общие понятия, размер кредитных вложений, средняя процентная ставка, ее динамика).
23. Кредитный рынок (валовой доход за пользование кредитами, возвратность кредита, кредитоотдача).
24. Финансы предприятия.
27. Статистическое изучение инвестиций.
28. Задачи статистики цен. Динамика средних цен.
29. Индексы цен Ласпейреса, Пааше, Фишера, Лоу. Использование индексов цен.
30. Показатели статистики уровня жизни населения.