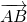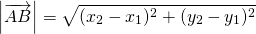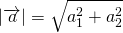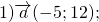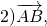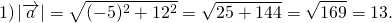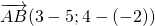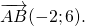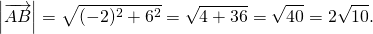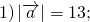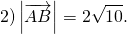Как рассчитывается длина вектора

Модуль вектора. Длина вектора.

Определение длины вектора

Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.

Формулы длины вектора

Формула длины вектора для плоских задач

В случае плоской задачи модуль вектора a = < a_x ; a_y > можно найти воспользовавшись следующей формулой:

Формула длины вектора для пространственных задач

В случае пространственной задачи модуль вектора a = < a_x ; a_y ; a_z > можно найти воспользовавшись следующей формулой:

Примеры задач на вычисление длины вектора

Примеры вычисления длины вектора для плоских задачи

Решение: | a | = √ 3 2 + (-4) 2 = √ 9 + 16 = √ 25 = 5.

Примеры вычисления длины вектора для пространственных задачи

Решение: | a | = √ 2 2 + 4 2 + 4 2 = √ 4 + 16 + 16 = √ 36 = 6.

Примеры вычисления длины вектора для пространств с размерностью большей 3

Решение: | a | = √ 1 2 + (-3) 2 + 3 2 + (-1) 2 = √ 1 + 9 + 9 + 1 = √ 20 = 2√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Длина вектора

Длина вектора (или модуль вектора или абсолютная величина вектора) — это длина отрезка, изображающего вектор.

с началом в точке A(x₁; y₁) и концом в точке B(x₂; y₂) длину находим по формуле расстояния между точками:

Соответственно, для вектора

(то есть длина вектора равна квадратному корню из суммы квадратов его координат).

Найти длину вектора:

2) Если нужно найти длину вектора, зная координаты его начала и конца, удобнее сначала найти координаты вектора:

Теперь найдём его длину:

Длина (модуль) нулевого вектора равна нулю.

Источник

Длина вектора

Определение

Длина вектора (модуль вектора) — длина направленного отрезка, которая определяет числовое значение вектора.

Обозначается, как \(\left|\vec AB\right|\)

Нахождение длины вектора

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Исходные данные \(a_x=5,\) \(a_y=-3\) подставляем в формулу и вычисляем.

Если же вектор находится в пространственной системе, то есть \(\vec a=\left(a_x;a_y;a_z\right),\) то для вычисления потребуется формула:

Узнать длину вектора \(\vec a\) по его координатам (2; 2; 4).

Подставляем данные координат из условия и вычисляем:

Длина вектора через координаты точек его начала и конца

В предыдущем разделе мы нашли длину вектора с помощью координат. Но если они неизвестны, то длину можно посчитать через координаты точек его начала и конца.

Если даны две точки: \(A\left(a_x;a_y\right) и B\left(b_x;b_y\right),\) то вектор \(\vec AB \) имеет координаты \(\left(b_x-a_x;b_y-a_y\right).\)

Отсюда следует формула:

Формула для трехмерного пространства выглядит следующим образом:

Нахождение длины вектора по теореме косинусов

Однако по условию задач координаты вектора не всегда известны. Тогда приходится искать иные пути решения.

Теорема косинусов — квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Вычислить длину вектора \(\vec BC.\)

Длина вектора \(\vec BC\) равна длине стороны BC треугольника ΔABC.

Исходные данные позволяют воспользоваться теоремой косинусов, так как длины стороны треугольника известны из условия (они равны длинам векторов \(\vec AB\) и \(\vec AC\) ). И угол между ними тоже известен.

\(BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos\angle\left(\vec AB,\vec AC\right)=2^2+4^2-2\cdot2\cdot4\cdot\cos\frac\pi4=4+16-8\sqrt2=20-8\sqrt2\)

Источник

Как найти длину вектора

Вы будете перенаправлены на Автор24

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Введем теперь, непосредственно, понятие длин вектора.

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

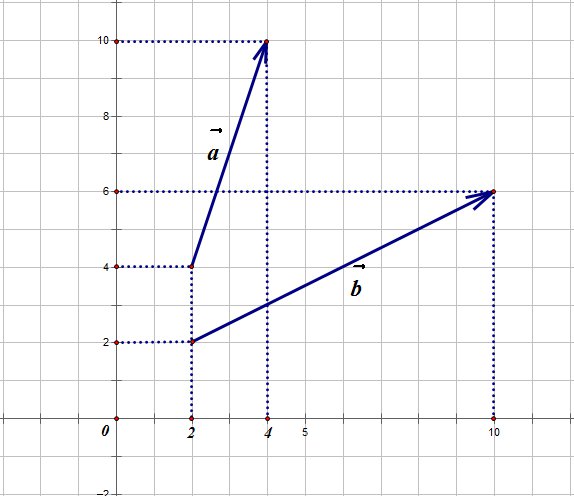
Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Готовые работы на аналогичную тему

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:

Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.

Первая сторона равняется:

Вторая сторона равняется:

Третья сторона равняется:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 07 2021

Источник

Онлайн калькулятор. Модуль вектора. Длина вектора

Этот онлайн калькулятор позволит вам очень просто найти длину вектора для плоских и пространственных задач.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление модуля вектора и закрепить пройденный материал.

Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам

Размерность вектора:

Форма представления вектора:

Инструкция использования калькулятора для вычисления длины вектора

Ввод даных в калькулятор для вычисления длины вектора (модуля вектора)

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел..

Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)

Вычисления длины вектора (модуля вектора)

Например, для вектора a = x; a_y; a_z> длина вектора вычисляется cледующим образом:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник