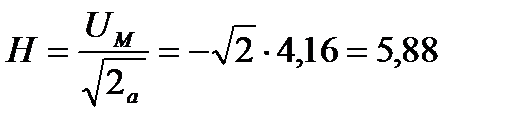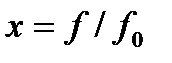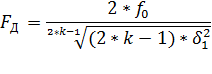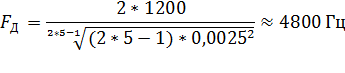Как рассчитывается частота дискретизации
Цифровое представление аналогового аудиосигнала. Краткий ликбез
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
Чем отличается цифровой аудиосигнал от аналогового?
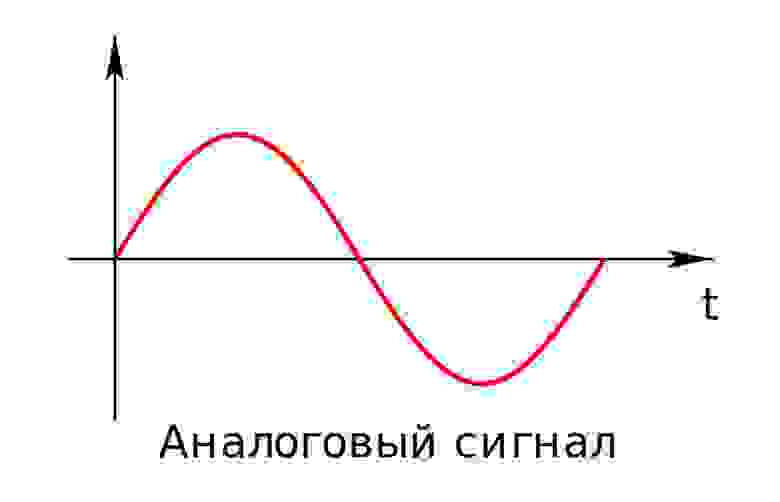
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
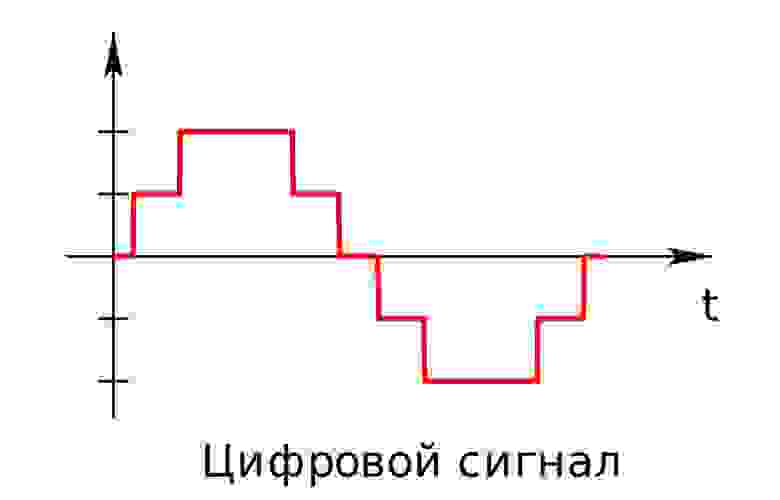
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
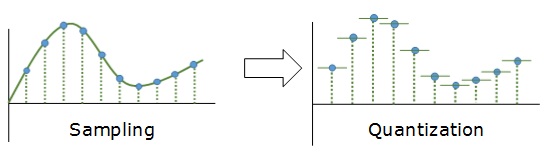
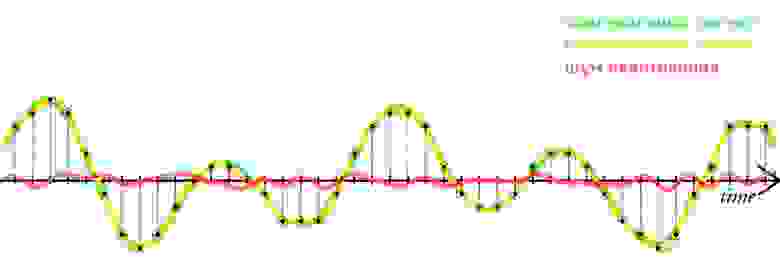
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
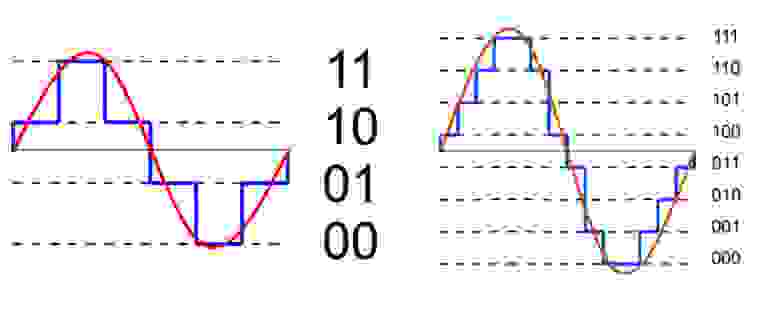
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
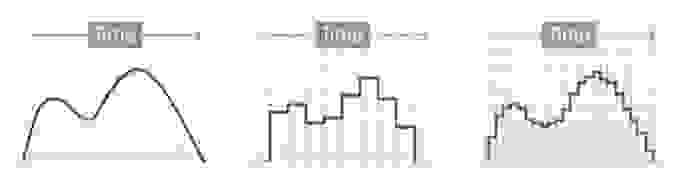
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
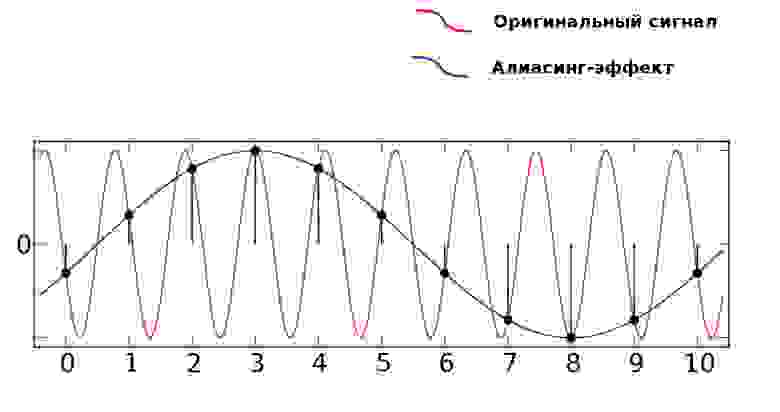
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от
100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
Несжатый (RAW) формат данных
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Расчет частоты дискретизации.
Курсовая работа
«Расчет параметров цифровой системы передачи непрерывного сообщения»
Преподаватель: Астрецов Д.В.
г. Екатеринбург, 2015
Содержание:
1.Распределение среднеквадратичной ошибки входных преобразований……4
2. Расчет частоты дискретизации………………………………………………. 4
4. Расчет числа разрядов двоичного кода……………………………………. 7
5. Расчёт длительности импульса двоичного кода……………………………..8
6.Расчет допустимой вероятности ошибки, вызванной действием помех…..9
8.Расчет отношения мощностей сигнала и шума, необходимых для обеспечения заданного качества приема……………………………………….11
9.Расчет энтропии источника сообщения……………………………………. 13
10. Расчет избыточности и информационной насыщенности сообщения……………………………………………………………………..…14
11. Расчет производительности источника сообщения и канала связи………15
12. Выбор сложных сигналов…………………………………………………. 16
Введение.
Основная задача курсовой работы – закрепление навыков расчёта характеристик системы передачи непрерывных сообщенийцифровыми сигналами. Кроме того, в процессе её выполнения студенты должны продолжить знакомство с учебной и монографической литературой по теории электрической связи, закрепить навыки выполнения технических расчётов с использованием персональных ЭВМ, а также отработку навыков и умений изложения результатов технических расчётов, составления и оформления технической документации. Такие навыки необходимы инженеру в той же степени, в какой необходимы навыки выполнения расчётов и других традиционных форм инженерной деятельности.
Исходные данные:
| 1.Вариант | |
| 2.Значение показателя степени k | |
| 3.Значение частоты f0,Гц | |
| 4.Значение относительной ошибки δ,% | 0,5 |
| 5.Вид модуляции | ЧМ |
| 6.Тип распределения |
1. Распределение относительной среднеквадратичной ошибки входных преобразований.
Распределение среднеквадратичной ошибки входных преобразований делиться на четыре составляющих: δ2 ограничение мгновенных значений исходного непрерывного процесса, δ1, вызванной временной дискретизацией, δ3квантования исходного непрерывного процесса и δ4искажений сообщения, вызванных действием помех.
δ= 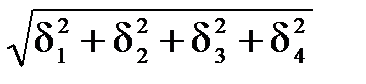
При заданном значении δ возможно много вариантов подбора значений слагаемых в формуле (1.1). Распределение Лапласа не является равномерным, следовательно, оно и неограниченно. Все 4 ошибки присутствуют и являются независимыми и случайными, из чего следует их равноценность:
Расчет пикфактора.
Определение пикфактора использует четыре вида законов распределения аналоговых сообщений. В нашем случае закон четвертого вида сообщения.
Рисунок 2. График зависимости эффективного значения относительной ошибки от пикфактора.
Сообщение четвертого вида имеет распределение:

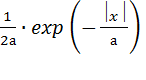
Дисперсия такого процесса равна:
Н=4,16 следовательно, пикфактор этого сообщения
4. Расчет числа Np двоичного кода.
Связь эффективного значения относительной ошибки квантования δ1 с числом разрядов Np двоичного кода при достаточно высоком числе уровней квантования, когда ошибку можно считать распределенной по закону равномерной плотности, определяется выражением:
Таким образом, задавшись допустимым значением относительной ошибки δ3, можно найти число разрядов двоичного кода, обеспечивающее заданную точность преобразования:
Np= E 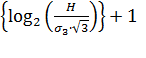
где E – целая часть дробного числа x.
Np= E 
В результате получили, что наш приемник сможет передавать 12 разрядный двоичный код.
Ширина спектра.
В результате манипуляции двоичная последовательность двоичных кодовых импульсов с различными начальными частотами может быть представлена суммой двух импульсных последовательностей с различными начальными частотами. Спектральная плотность мощности такой последовательности имеет вид 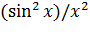
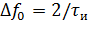
На практике ширина спектра определяется полосой частот, в которой сосредоточено 80-90 % мощности сигнала.
При условии, что 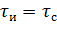
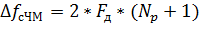
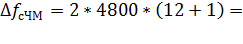
Заключение.
В результате курсовой работы мы закрепили навыки по темам анализ систему передачи непрерывных сообщений цифровыми методами, расчет характеристик помехоустойчивости и других показателей качества передачи информации по каналу связи с помехами. Разработали структурную схему системы передачи непрерывного сообщения в цифровой форме.
По теореме Шеннона, если производительность источника сообщений меньше пропускной способности канала, то существует такая процедура кодирования и декодирования, при которой вероятность ошибочного декодирования будет меньше допустимой. Поэтому для повышения помехоустойчивости приема используется помехоустойчивое кодирование.
Сведем в таблицу 1 результаты, полученные в ходе выполнения курсовой работы:
Таблица 1. Результаты расчетов:
| Величина | Значение |
| 1. Значение пик-фактора H | 5,88 |
| 2. Значение частоты дискретизации Fд, Гц | |
| 3. Число разрядов двоичного кода Nр | |
| 4. Длительность импульса, мкс | |
| 5.Ширина спектра Δfc, кГц | 124,8 |
| 6. Расчёт энтропии Н3(x), бит/символ | 10,114 |
| 7. Информационная эффективностьIэф | 0,843 |
| 8. Избыточность R(x) | 0,157 |
| 9. Производительность источника сообщений Vn, бит/с | 18205,2 |
| 10. Требуемое значение отношения сигнал/шум для обеспечения пропускной способности канала связи | |
| 11. Требуемое отношение q 2 при оптимальном когерентном приёме | 28,6 |
| 12. Требуемое отношение q 2 при оптимальном некогерентном приёме | 32,36 |
Список литераторы.
2. Теория электрической связи. Учебное пособие / А.В. Паршин, Е.А. Субботин / СибГУТИ, Екатеринбург, 2005г.
Приложения
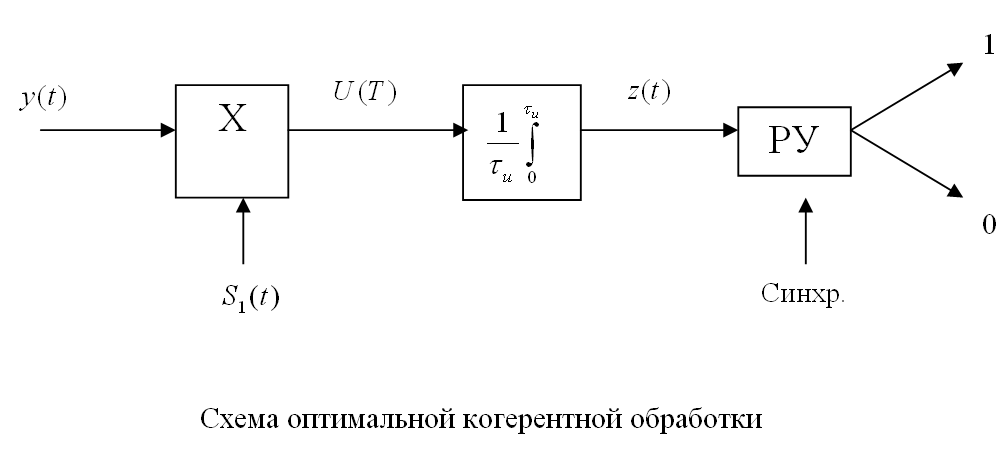
Структурные схемы оптимального когерентного и некогерентного различителей бинарных сигналов.
Курсовая работа
«Расчет параметров цифровой системы передачи непрерывного сообщения»
Преподаватель: Астрецов Д.В.
г. Екатеринбург, 2015
Содержание:
1.Распределение среднеквадратичной ошибки входных преобразований……4
2. Расчет частоты дискретизации………………………………………………. 4
4. Расчет числа разрядов двоичного кода……………………………………. 7
5. Расчёт длительности импульса двоичного кода……………………………..8
6.Расчет допустимой вероятности ошибки, вызванной действием помех…..9
8.Расчет отношения мощностей сигнала и шума, необходимых для обеспечения заданного качества приема……………………………………….11
9.Расчет энтропии источника сообщения……………………………………. 13
10. Расчет избыточности и информационной насыщенности сообщения……………………………………………………………………..…14
11. Расчет производительности источника сообщения и канала связи………15
12. Выбор сложных сигналов…………………………………………………. 16
Введение.
Основная задача курсовой работы – закрепление навыков расчёта характеристик системы передачи непрерывных сообщенийцифровыми сигналами. Кроме того, в процессе её выполнения студенты должны продолжить знакомство с учебной и монографической литературой по теории электрической связи, закрепить навыки выполнения технических расчётов с использованием персональных ЭВМ, а также отработку навыков и умений изложения результатов технических расчётов, составления и оформления технической документации. Такие навыки необходимы инженеру в той же степени, в какой необходимы навыки выполнения расчётов и других традиционных форм инженерной деятельности.
Исходные данные:
| 1.Вариант | |
| 2.Значение показателя степени k | |
| 3.Значение частоты f0,Гц | |
| 4.Значение относительной ошибки δ,% | 0,5 |
| 5.Вид модуляции | ЧМ |
| 6.Тип распределения |
1. Распределение относительной среднеквадратичной ошибки входных преобразований.
Распределение среднеквадратичной ошибки входных преобразований делиться на четыре составляющих: δ2 ограничение мгновенных значений исходного непрерывного процесса, δ1, вызванной временной дискретизацией, δ3квантования исходного непрерывного процесса и δ4искажений сообщения, вызванных действием помех.
δ= 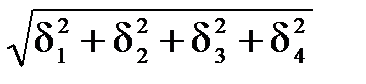
При заданном значении δ возможно много вариантов подбора значений слагаемых в формуле (1.1). Распределение Лапласа не является равномерным, следовательно, оно и неограниченно. Все 4 ошибки присутствуют и являются независимыми и случайными, из чего следует их равноценность:
Расчет частоты дискретизации.
По результатам распределения Относительной среднеквадратичной ошибки рассчитывается частота дискретизации (Fд).
По теореме Котельникова :
Эффективное значение относительной ошибки временной дискретизации сообщения x(t) определяется равенством:
δ1= 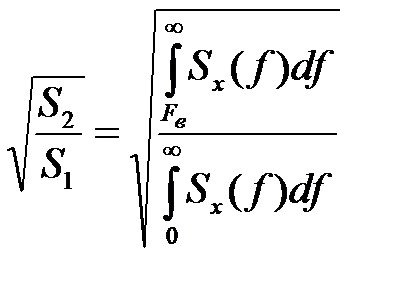
где Fд – частота дискретизации;
Sx(f) – спектральная плотность мощности сообщения x(t);
S1 – площадь всей фигуры (Рисунок 1);
| Sx(f) |
| f0 |
| Fв |
| f |
| Sx(0) |
S2 – площадь заштрихованной части (Рисунок 1).
Рисунок 1. Cпектральная плотность сигнала
В задании на проектирование форма спектральной плотности мощности сообщения определена равенством
Sx(f)= 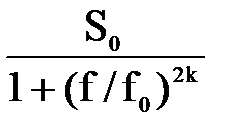
где S0 – спектральная плотность мощности сообщения на нулевой частоте;
k – параметр, характеризующий порядок фильтра, формирующего сообщение;
f0 – частота, определяющая ширину спектра сообщения по критерию снижения Sx(f) в два раза по сравнению с её значением на нулевой частоте Sx(0).
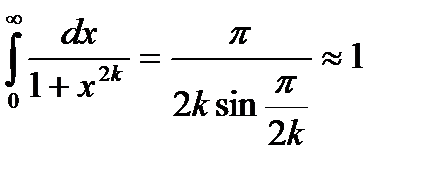
где

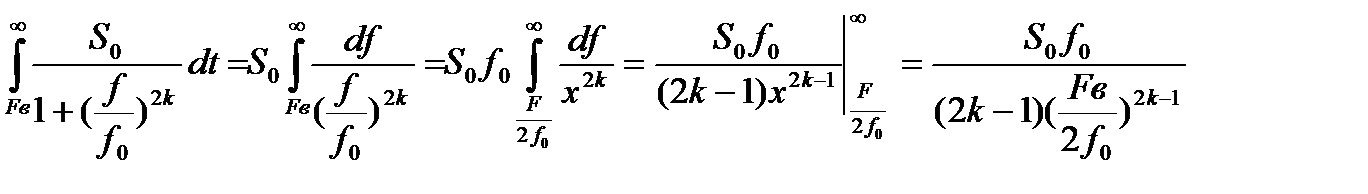

Пользуясь формулой (2.7) можно вычислить частоту временной дискретизации Fд (Гц):
Расчет пикфактора.
Определение пикфактора использует четыре вида законов распределения аналоговых сообщений. В нашем случае закон четвертого вида сообщения.
Рисунок 2. График зависимости эффективного значения относительной ошибки от пикфактора.
Сообщение четвертого вида имеет распределение:

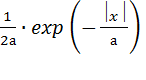
Дисперсия такого процесса равна:
Н=4,16 следовательно, пикфактор этого сообщения
4. Расчет числа Np двоичного кода.
Связь эффективного значения относительной ошибки квантования δ1 с числом разрядов Np двоичного кода при достаточно высоком числе уровней квантования, когда ошибку можно считать распределенной по закону равномерной плотности, определяется выражением:
Таким образом, задавшись допустимым значением относительной ошибки δ3, можно найти число разрядов двоичного кода, обеспечивающее заданную точность преобразования:
Np= E 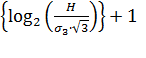
где E – целая часть дробного числа x.
Np= E 
В результате получили, что наш приемник сможет передавать 12 разрядный двоичный код.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.