Как рассчитать средневзвешенное содержание
Средневзвешенное значение — формула в Excel
В одной из предыдущих статей мы обсудили три основные функции для вычисления среднего в Excel, которые очень просты и просты в использовании.
Но что, если некоторые значения более важны, чем другие, и, следовательно, вносят больший вклад в конечное среднее значение? Например, если вы участвуете в экзаменах и все экзамены имеют одинаковый вес, они одинаково важны, то для вас важно именно среднее значение оценки.
Однако в реальной жизни это не всегда так. Например, если вы изучаете программирование, то насколько важны для вас оценки по истории и физкультуре по сравнению с оценками по профильным дисциплинам?
Некоторые задачи всегда важнее других. Некоторые экзамены важнее других.
В таких ситуациях вам как раз и необходимо рассчитывать средневзвешенное значение.
Хотя Microsoft Excel не предоставляет специальной функции взвешенного среднего, он предоставляет несколько других, которые окажутся полезными в ваших вычислениях, что показано в следующих примерах.
Что такое средневзвешенное значение?
Оно является своего рода средним арифметическим, в котором некоторые элементы набора данных имеют большую значимость, чем другие. Другими словами, каждому исходному показателю присваивается определенный вес.
В математике и статистике вы вычисляете взвешенное среднее значение, умножая каждое число в наборе на его вес, затем складываете произведения и делите итог сложения произведений на сумму всех весомостей.
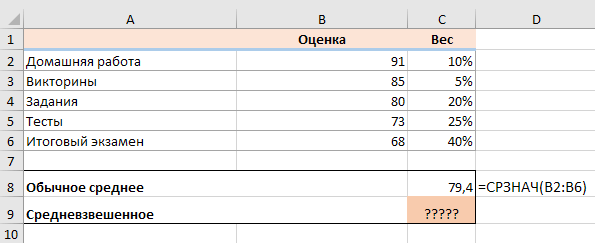
В этом примере, чтобы посчитать средневзвешенную итоговую оценку, вы умножаете каждый полученный балл на соответствующий процент (преобразованный в десятичную дробь), складываете эти 5 произведений вместе и делите это число на итог сложения пяти весов:
((91 * 0,1) + (85 * 0,05) + (80 * 0,2) + (73 * 0,25) + (68 * 0,4)) / (0,1 + 0,05 + 0,2 + 0,25 + 0,4) = 74,8
Формулы для средневзвешенного значения в Excel
В Microsoft Excel взвешенное среднее рассчитывается с использованием того же подхода, но с гораздо меньшими усилиями, поскольку функции Excel выполнят большую часть работы за вас.
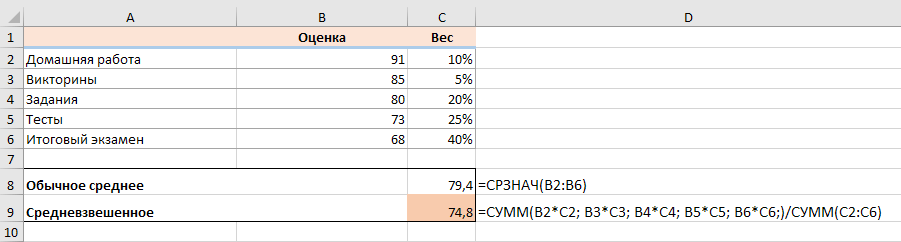
Пример 1. Функция СУММ.
По сути, он выполняет те же вычисления, что и описанные выше, за исключением того, что вы предоставляете ссылки на ячейки вместо чисел.
Посмотрите на рисунок чуть ниже: формула возвращает точно такой же результат, что и вычисления, которые мы делали минуту назад. Обратите внимание на разницу между нормальным средним, возвращаемым при помощи СРЗНАЧ в C8, и средневзвешенным (C9).
Несмотря на то, что формула эта очень проста и понятна, но она не подходит, если вы хотите усреднить большое количество элементов. Ведь придётся перечислять множество аргументов, что довольно утомительно.
В этом случае вам лучше использовать функцию СУММПРОИЗВ (SUMPRODUCT в английской версии). Об этом – ниже.
Пример 2. Функция СУММПРОИЗВ
Она идеально подходит для нашей задачи, так как предназначена для сложения произведений чисел. А это именно то, что нам нужно.
Таким образом, вместо умножения каждого числа на показатель его значимости по отдельности, вы предоставляете два массива в формуле СУММПРОИЗВ (в этом контексте массив представляет собой непрерывный диапазон ячеек), а затем делите результат на итог сложения весов:
= СУММПРОИЗВ(диапазон_значений ; диапазон_весов ) / СУММ( диапазон_весов )
Итак, формула умножает 1- е число в массиве 1 на 1- е в массиве 2 (в данном примере 91 * 0,1), а затем перемножает 2- е число в массиве 1 на 2- е в массиве 2 (85 * 0,15). в этом примере) и так далее. Когда все умножения выполнены, Эксель складывает произведения. Затем делим полученное на итог весов.
Чтобы убедиться, что функция СУММПРОИЗВ дает правильный результат, сравните ее с формулой СУММ из предыдущего примера, и вы увидите, что числа идентичны.
В нашем случае сложение весов дает 100%. То есть, это просто процент от итога. В таком случае верный результат может быть получен также следующими способами:
Но при использовании функции СУММ или СУММПРОИЗВ веса совершенно не обязательно должны составлять 100%. Однако, они также не должны быть обязательно выражены в процентах.
Например, вы можете составить шкалу приоритета / важности и назначить определенное количество баллов для каждого элемента, что и показано на следующем рисунке:
Видите, в этом случае мы обошлись без процентов.
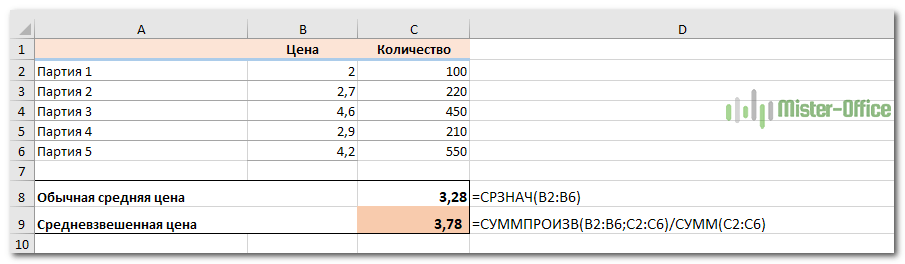
Пример 3. Средневзвешенная цена.
Еще одна достаточно часто встречающаяся проблема – как рассчитать средневзвешенную цену товара. Предположим, мы получили 5 партий товара от различных поставщиков. Мы будем продавать его по одной единой цене. Но чтобы ее определить, нужно знать среднюю цену закупки. В тот здесь нам и пригодится расчет средневзвешенной цены. Взгляните на этот простой пример. Думаю, вам все понятно.
Итак, средневзвешенная цена значительно отличается от обычной средней. На это повлияли 2 больших партии товара по высокой цене. А формулу применяем такую же, как и при расчете любого взвешенного среднего. Перемножаем цену на количество, складываем эти произведения, а затем делим на общее количество товара.
Ну, это все о формуле средневзвешенного значения в Excel.
Средневзвешенная формула
Формула взвешенного среднего (Содержание)
Средневзвешенная формула
Среднее арифметическое = (X1 + X2 + X3 ………. + Xn) / n
Среднее арифметическое = X1 / n + X2 / n + ………………… + Xn / n
Таким образом, все точки данных имеют одинаковый вес и задаются как 1 / n.
Но допустим, что веса различны и определяются как (w1, w2, w3 …………, wn). Таким образом, формула для средневзвешенного значения определяется как:
Weighted Mean = w1*X1 + w2*X2 + w3*X3……………+ wn*Xn
Примеры формулы взвешенного среднего (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять формулу взвешенного среднего.
Допустим, у вас есть набор данных с 10 точками данных, и мы хотим рассчитать средневзвешенное значение для этого.
Набор данных: (4, 6, 8, 9, 22, 83, 98, 45, 87, 10)
Вес: (20%, 15%, 10%, 10%, 5%, 3%, 2%, 7%, 5%, 13%)
Сначала мы рассчитываем произведение набора данных и весов.
Результат будет таким, как указано ниже.
Точно так же мы рассчитали для всех данных.
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Допустим, все веса равны, т.е. 10% для каждого набора данных.
Сначала мы рассчитываем произведение набора данных и весов.
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Среднее арифметическое рассчитывается по формуле, приведенной ниже
Среднее арифметическое = (сумма всех точек данных) / количество точек данных
Поэтому, когда все веса равны, среднее арифметическое такое же, как среднее взвешенное
Допустим, у вас есть портфель, в котором у вас есть акции, облигации и товары. Таким образом, в основном у нас есть портфель, в который мы инвестировали в акции, облигации и товары. Ниже приведены веса / пропорции каждого инструмента в вашем портфеле:
Средневзвешенное значение рассчитывается по формуле, приведенной ниже
Средневзвешенное значение = w1 * X1 + w2 * X2 + w3 * X3 …………… + wn * Xn
Простая средняя доходность портфеля рассчитывается по формуле, приведенной ниже
Простая средняя доходность портфеля = сумма возвратов / количество товаров
объяснение
Актуальность и использование формулы взвешенного среднего
Калькулятор формулы взвешенного среднего
Вы можете использовать следующий калькулятор взвешенного среднего
Рекомендуемые статьи
Средневзвешенное
Опубликовано 22.05.2020 · Обновлено 22.05.2021
Что такое Средневзвешенное?
Средневзвешенное значение – это расчет, который учитывает различную степень важности чисел в наборе данных. При вычислении средневзвешенного значения каждое число в наборе данных умножается на заранее определенный вес перед окончательным расчетом.
Средневзвешенное значение может быть более точным, чем простое среднее, в котором всем числам в наборе данных присваивается одинаковый вес.
Понимание средневзвешенных значений
При вычислении простого среднего или среднего арифметического все числа обрабатываются одинаково, и им присваивается одинаковый вес. Но средневзвешенное значение присваивает веса, которые заранее определяют относительную важность каждой точки данных.
Ключевые моменты
Средневзвешенное значение чаще всего вычисляется для выравнивания частоты значений в наборе данных. Например, опрос может собрать достаточно ответов от каждой возрастной группы, чтобы считаться статистически достоверным, но возрастная группа 18-34 может иметь меньше респондентов, чем все остальные, по отношению к их доле в населении. Команда опроса может взвесить результаты возрастной группы 18-34 года, чтобы их взгляды были представлены пропорционально.
Однако значения в наборе данных могут быть взвешены по другим причинам, кроме частоты появления. Например, если ученики в танцевальном классе оцениваются по навыкам, посещаемости и манерам, оценка по навыкам может иметь больший вес, чем другие факторы.
В любом случае при средневзвешенном значении каждое значение точки данных умножается на назначенный вес, который затем суммируется и делится на количество точек данных.
В средневзвешенном значении окончательное среднее число отражает относительную важность каждого наблюдения и, таким образом, является более информативным, чем простое среднее. Это также имеет эффект сглаживания данных и повышения их точности.
Взвешивание портфеля акций
Инвесторы обычно создают позицию в акции в течение нескольких лет. Это затрудняет отслеживание стоимости этих акций и их относительных изменений в стоимости.
Инвестор может рассчитать средневзвешенную цену акций, уплаченных за акции. Для этого умножьте количество акций, приобретенных по каждой цене, на эту цену, сложите эти значения и затем разделите общую стоимость на общее количество акций.
Краткая справка
Средневзвешенное значение достигается путем предварительного определения относительной важности каждой точки данных.
Например, предположим, что инвестор приобретает 100 акций компании в первый год по цене 10 долларов США и 50 акций той же компании во второй год по цене 40 долларов США. Чтобы получить средневзвешенное значение уплаченной цены, инвестор умножает 100 акций на 10 долларов для первого года и 50 акций на 40 долларов для второго года, а затем складывает результаты, чтобы получить в сумме 3000 долларов. Затем общая сумма, уплаченная за акции, в данном случае 3000 долларов, делится на количество акций, приобретенных за оба года, 150, чтобы получить средневзвешенную цену в размере 20 долларов.
Теперь это среднее значение взвешивается по количеству акций, приобретенных по каждой цене, а не только по абсолютной цене.
Примеры средневзвешенных значений
Средневзвешенные значения появляются во многих областях финансов, помимо покупной цены акций, включая доходность портфеля, учет запасов и оценку.
Когда фонд, владеющий несколькими ценными бумагами, увеличивается на 10 процентов за год, эти 10 процентов представляют собой средневзвешенную доходность фонда по отношению к стоимости каждой позиции в фонде.
Для учета запасов средневзвешенная стоимость запасов учитывает колебания цен на товары, например, в то время как методы LIFO (последний пришел – первый ушел) или FIFO (первый пришел – первый ушел) придает большее значение времени, чем стоимости.
При оценке компаний, чтобы определить, правильно ли установлена цена на их акции, инвесторы используют средневзвешенную стоимость капитала (WACC) для дисконтирования денежных потоков компании. WACC взвешивается на основе рыночной стоимости долга и капитала в структуре капитала компании.
Средневзвешенная формула
Средневзвешенная формула (Содержание)
Средневзвешенная формула
Формула для расчета средневзвешенного значения выглядит следующим образом:
Примеры средневзвешенной формулы
Давайте рассмотрим несколько примеров, чтобы понять формулу взвешенного среднего:
Пример № 1
Предположим, что Ананд вложил деньги в следующем пропорциональном соотношении: 40% в инвестиции A, 20% в инвестиции B и 40% в инвестиции C. Эти инвестиции имеют норму прибыли следующим образом: инвестиции A как 15%, инвестиции B как 10 %, а инвестиции C как 20% соответственно. Нам нужно рассчитать средневзвешенное значение для норм прибыли, которые получит Ананд.
Используя формулу средневзвешенного, мы получаем
Это показывает, что Ананд будет получать средневзвешенную доходность 16% от инвестиций A, B & C.
Пример № 2
Предположим, что Ананд записался на курс по математике, его итоговая оценка будет определяться на основе следующих категорий: тесты 30%, итоговый экзамен 40%, тесты 15% и домашние задания 15%.
Ананд набрал следующие оценки в каждой категории: тесты-80, итоговый экзамен-65, тесты-85, домашнее задание-90. Теперь нам нужно узнать общий балл Ананда.
Чтобы рассчитать средневзвешенное значение с процентами, каждое значение категории должно быть сначала умножено на процент. Затем все эти новые значения должны быть добавлены вместе.
У нас есть Относительные веса для следующих категорий:
И, Значение (Знаки) для категорий как
Используя формулу средневзвешенного, мы получаем
Это показывает, что общий балл Ананда составляет 76%.
Пример № 3
Давайте предположим, что Jagriti вложили деньги в акции разных компаний. Портфель Jagriti включает 30% в Акции A, 15% в Акции B, 30% в Акции C и оставшиеся 25% в Акции D. Ожидаемая доходность в соответствии с текущей рыночной ситуацией по этим Акциям следующая: Рентабельность Акции A составляет 15%, доходность на складе B составляет 12%, доходность на складе C составляет 17%, а доходность на акции D составляет 16% соответственно. Джагрити хочет рассчитать свою среднюю доходность портфеля в соответствии с текущей ситуацией на рынке.
Используя формулу средневзвешенного, мы получаем
Это показывает, что Jagriti будет получать средневзвешенную доходность 15, 4% от Портфеля акций A, B, C и D.
Пояснение формулы средневзвешенного
Формула взвешенного среднего используется для расчета среднего значения для определенного набора чисел с различными уровнями релевантности. Веса должны быть представлены с точки зрения общей релевантности в процентах. Взятые веса должны быть равны 100% или 1.
Чтобы рассчитать средневзвешенную формулу, нам нужны относительный вес и стоимость.
Значение и использование формулы средневзвешенного
Средневзвешенное значение используется в различных финансовых формулах. Несколько примеров средневзвешенной беты и средневзвешенной стоимости капитала (WACC).
Мы знакомы с идеей нахождения среднего или среднего значения для ряда предметов. Мы можем просто сложить значения всех элементов и разделить их на общее количество элементов для расчета среднего значения. Это будет работать только в том случае, если все элементы имеют одинаковый вес. Например, для расчета среднемесячных счетов за мобильный телефон за год мы можем просто сложить итоговые суммы счетов за последние двенадцать месяцев и поделить их на двенадцать, а затем мы можем получить приблизительное представление о среднем оплачиваемом счете, так как мобильный Цикл счета примерно для того же периода времени, т. е. одного месяца.
Теперь предположим, что вы хотите рассчитать текущую среднюю оценку за курс в вашем классе по математике. Обычно большинство классов присваивают экзаменам другой вес, нежели домашние задания, внутренние тесты и соревнования. В этом случае вам необходимо рассчитать средневзвешенное значение, которое учитывает конкретный вес каждой темы для расчета вашей оценки за курс.
Если у компании наблюдаются значительные колебания продаж из-за производства сезонного продукта, они могут использовать формулу средневзвешенного значения. И компания хочет рассчитать среднее значение для своих переменных расходов, затем компания может использовать формулу взвешенного среднего и принять продажи в качестве веса, чтобы лучше понять свои расходы. И можете сравнить количество, которое они производят или продают.
Средневзвешенный калькулятор
Вы можете использовать следующий калькулятор взвешенного среднего
Средневзвешенная формула в Excel (с шаблоном Excel)
Здесь мы сделаем тот же пример формулы средневзвешенного значения в Excel. Это очень легко и просто. Вам необходимо предоставить два входа: относительный вес и норму прибыли.
Вы можете легко рассчитать средневзвешенное значение, используя формулу в предоставленном шаблоне.
Средневзвешенная доходность от инвестиций A, B & C рассчитывается как:
Общий балл Ананда рассчитывается как:
Вес Средний возраст возврата из Портфеля акций A, B, C и D рассчитывается как:
Рекомендуемые статьи
Средневзвешенные акции и акции в обращении
Опубликовано 10.06.2021 · Обновлено 12.06.2021
Понимание разницы между средневзвешенными акциями и акциями в обращении жизненно важно для инвесторов, пытающихся создать портфель, который будет работать в соответствии с их ожиданиями. Эти два расчета предоставляют информацию о том, насколько хорошо компания работает с течением времени.
Акции в обращении
Акции, находящиеся в обращении, относятся к акциям, которые в настоящее время принадлежат инвесторам. Сюда также входят акции, принадлежащие широкой публике, и акции с ограниченным доступом, принадлежащие должностным лицам компании и инсайдерам. Количество находящихся в обращении акций изменяется, если компания выпускает новые акции, выкупает существующие акции или если опционы сотрудников конвертируются в акции.
Средневзвешенное количество акций
В средневзвешенные акций в обращении, или средневзвешенное акций в обращении, является расчет, который принимает во внимание любые изменения в количестве размещенных акций за определенный отчетный период. Инвесторы, вкладывая средства на длительный срок, часто формируют позицию в акции на несколько лет.
Цены на акции меняются ежедневно, поэтому желательно отслеживать стоимость акций, накопленных за многие годы. Если инвестор хочет рассчитать средневзвешенную цену, уплаченную за акции, он должен умножить количество акций, приобретенных по каждой цене, на эту цену, сложить эти значения, а затем разделить общую стоимость на общее количество акций.
В общем, средневзвешенное значение – это среднее значение, вычисленное путем усреднения каждой величины по назначенному весу для определения относительной важности каждой величины.
Средневзвешенное количество акций определяется путем умножения количества акций в обращении на процентную долю отчетного периода, для которого это количество применяется для каждого периода. Другими словами, в формуле берется количество акций, находящихся в обращении в течение каждого месяца, взвешенное по количеству месяцев, в течение которых эти акции находились в обращении.
Средневзвешенная цена на акцию
Инвесторы могут использовать средневзвешенные значения, если они сформировали позицию по определенной акции за период. Учитывая постоянно меняющиеся цены на акции, инвестор рассчитает средневзвешенную цену акций, уплаченных за акции.
Чтобы рассчитать средневзвешенную стоимость одной акции, инвестор может умножить количество акций, приобретенных по каждой цене, на эту цену, сложить эти значения, а затем разделить общую стоимость на общее количество акций.
Средневзвешенные значения также могут использоваться в других аспектах финансов, включая расчет доходности портфеля, учет запасов и оценку.
Средневзвешенное количество акций в обращении
Средневзвешенное количество акций в обращении используется для расчета ключевых финансовых показателей, таких как прибыль на акцию (EPS). Управленческие и финансовые аналитики уделяют особое внимание прибыли на акцию, поскольку она представляет собой прибыль, оставшуюся от операций, доступную акционерам. Например, базовая прибыль на акцию рассчитывается следующим образом:
Базовая прибыль на акцию = базовые средневзвешенные акции
С другой стороны, базовые средневзвешенные акции представляют собой вышеупомянутые средневзвешенные акции, находящиеся в обращении, за вычетом разводнения опционов на акции за определенный период. Для базовых средневзвешенных акций «базовые» по сути означает неразводняющие.
Разбавление происходит, когда компания выпускает дополнительные акции, которые уменьшают пропорциональную долю владения существующего инвестора в компании. Использование разводненных акций более информативно, чем использование базовых акций, потому что, если ценные бумаги конвертируются в обыкновенные акции, другими словами, происходит разводнение, доля инвестора в компании или их доля в общем круге акций сокращается.
Компаниям с простой структурой капитала необходимо сообщать только базовую прибыль на акцию. Те, у кого сложная структура (те, у которых есть потенциально разводняющие ценные бумаги), должны сообщать как базовую прибыль на акцию, так и разводненную прибыль на акцию.