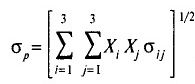Как рассчитать риск портфеля
Что такое современная теория портфеля
Поиск оптимального способа распределения активов
Хоть теория и современная, первому ее упоминанию уже 70 лет.
В основе MPT лежит тезис о том, что риск и доходность взаимосвязаны. Это означает, что желание инвестора получить более высокую доходность непременно повышает уровень риска, а между двумя портфелями с одинаковой ожидаемой доходностью рационально выбирать менее рискованный вариант.
Под риском в теории понимается волатильность портфеля — то есть то, насколько изменчива его цена. Математически волатильность выражается через статистический показатель, который называется стандартным отклонением. Пример его расчета я приводил в статье про всепогодную стратегию.
MPT утверждает, что для каждого уровня риска есть соответствующая комбинация активов, которая максимизирует доход, — такой портфель называется оптимальным. Другая идея MPT заключается в том, что за счет диверсификации по различным классам активов можно сгладить волатильность портфеля. Таким образом, мы либо максимизируем доход при заданном уровне риска, либо минимизируем риск при целевой доходности.
Рассмотрим, как это работает.
Что такое эффективная граница
На диаграмме ниже представлена так называемая эффективная граница для портфелей, составленных из акций и среднесрочных казначейских облигаций в разных пропорциях.
Оптимальные портфели расположены на фиолетовой линии. Варианты выше нее недостижимы: не существует портфелей с таким отношением доходности к риску. А портфели ниже линии неэффективны: они либо дают доходность ниже ожидаемой, либо подразумевают больший риск.
Оптимизация портфеля означает поиск компромисса между риском и прибылью. Поэтому инвестору важно заранее определиться с желаемой доходностью и комфортным для себя уровнем риска. Повторюсь, что речь здесь идет про волатильность, с которой готов мириться инвестор. Этот риск не означает полной потери актива, но может включать ее, например если компания обанкротится. Но диверсификация портфеля обычно снимает этот вопрос.
Виды рисков инвестиционного портфеля
При составлении инвестиционного портфеля для достижения стабильных высоких положительных результатов доходности необходимо уметь заранее рассчитывать возможные риски.
Риск — контролируемая и поддающаяся управлению величина. Стоит сразу отметить, что риском можно считать не только недополучение искомой прибыли. К нему относятся также другие неожиданные «сюрпризы» при получении не просчитанной заранее сверхвысокой доходности, поскольку подобные отклонения могут возникнуть и в обратную сторону. В этой статье мы разберем, что именно можно считать риском, и какие виды рисков существуют.
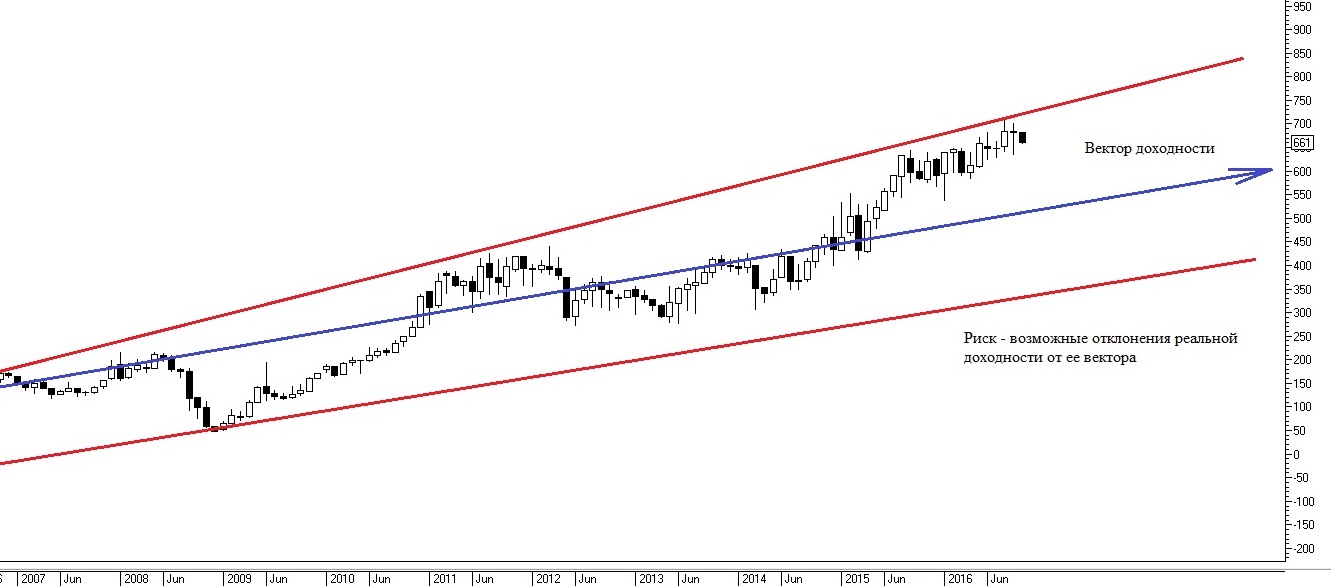
Доходность — это векторная величина, показывающая общее направление изменения цены актива (или портфеля) и рассчитанная из истории котировок. Риск, в свою очередь, представляет собой своего рода меру колебаний цены вокруг этого вектора (стандартное отклонение).
Инвестиционный портфель состоит из определенного количества ценных бумаг, каждая из которых обладает своими показателями риска/доходности. Причем как риск, так и доходность активов в портфеле усредняются с учетом их весовой доли. Формула риска инвестиционного портфеля (стандартное отклонение портфеля) как раз и включает в свой расчет сумму произведений весовых долей и стандартных отклонений бумаг, входящих в портфель, а также вычисление квадратного корня из полученного числа, где:
То есть происходит своего рода усреднение мер колебаний относительно вектора доходности по всем бумагам портфеля с весовыми коэффициентами этих бумаг.
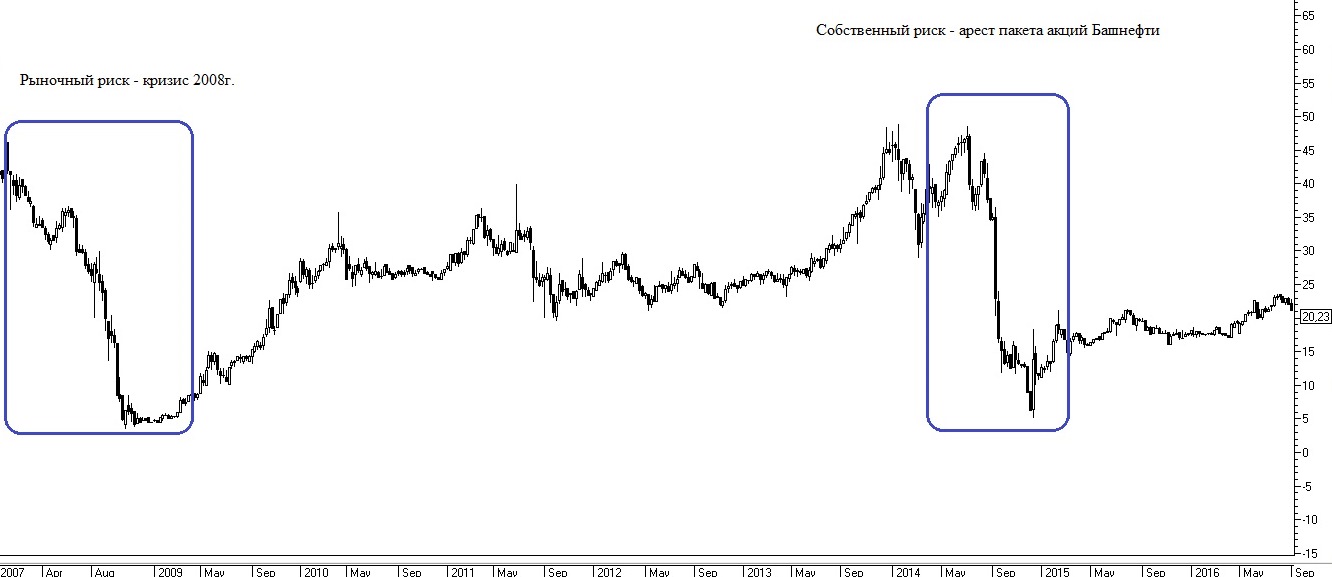
В чем же может заключаться риск инвестиционного портфеля? Начнем с того, что существуют два основных вида риска: рыночный и собственный. Общее положение дел в мировой экономике — программы количественного смягчения, введение/снятие санкций, войны, кризисы и так далее — влияют на все активы в большей или меньшей степени. Это и есть рыночный риск. Также, помимо общих экономических тенденций в каждой отдельно взятой компании, могут появляться новости — как неожиданно хорошие, так и плохие — которые будут давать сильное отклонение от изначального ценового движения.
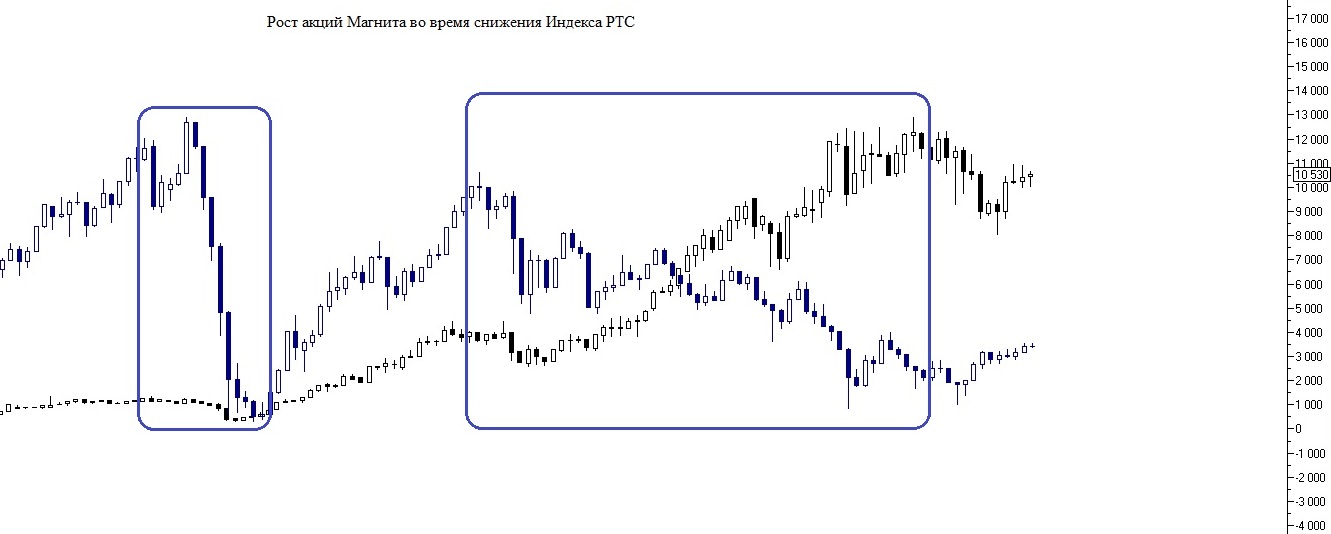
Общие экономические тенденции, безусловно, влияют на ценные бумаги, но рыночный риск тоже можно контролировать, как и любой другой риск инвестиционного портфеля. Нередко аналитики говорят, что на важных поддержках по индексам (барометрам экономики) целесообразно включать в портфель сильные акции. Суть этих высказываний — в том, что когда по индексам начинается рост от важных поддержек, бумаги по «широкому фронту» тоже склонны расти — какие-то больше, какие-то меньше.
Также целесообразно включать именно сильные бумаги, то есть те, которые имеют свойство расти быстрее рыночных индексов (в случае роста последних) и снижаться медленнее при индексных падениях (либо стоять на месте или слабо расти). Дать подобную оценку можно исходя из истории цен того или иного актива путем сравнения с индексом. Следует понять, насколько хорошо бумага умеет сопротивляться индексным снижениям. А затем, исходя из постулата о повторяемости истории, включить такие бумаги в инвестиционный портфель.
Оценка риска инвестиционного портфеля с точки зрения собственного риска приводит к мысли о важности диверсификации. Чем больше активов в портфеле, тем меньше доля каждого из них. Так как собственный риск не является рыночным, то его реализация является лишь частным случаем и не наступает по широкому фронту. Иными словами, если бумаг в инвестиционном портфеле мало, и какая-то из них начинает экстремально отклоняться от своего вектора доходности, ее удельный вклад в портфель получится большим. Если бумаг много, даже при падении одной из них на 20%, при доле 5%, портфель просядет всего на 1%, что легко сможет компенсироваться ростом остальных активов.
Таким образом, благодаря высокой диверсификации риск инвестиционного портфеля снижается, что сглаживает общую доходность и делает ее более плавной, поскольку бумаги начинают компенсировать колебания друг друга. Также высокая диверсификация способствует повышению управляемости портфелем. Вы с легкостью можете заменить актив, не оправдавший ожиданий инвестора, на более перспективный, складывая доходность портфеля из элементов общей рыночной мозаики.
Получается, что рыночный риск сокращается путем включения в портфель бумаг, показывающих высокую сопротивляемость рыночным снижениям, а собственный риск снижается диверсификацией.
Оценка рисков инвестиционного портфеля — то, с чего начинается построение доходных портфелей. Научившись оценивать риск инвестиционного портфеля, трейдер-любитель переходит в разряд профессионалов. Следует помнить, что риск присутствует всегда и во всем, но им можно управлять, а значит — минимизировать.
Не терпится внедрить наши советы в работу? Откройте счёт в компании «Открытие Брокер» – здесь можно торговать как самостоятельно, так и под руководством профессионалов. А если в процессе появятся вопросы – задайте их через форму обратной связи. Постараемся ответить как можно подробнее!
Как считать индикаторы инвестиционной привлекательности активов
На примере портфеля Уоррена Баффетта
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
((1 + 20%) × (1 − 10%) × (1 + 30%)) 1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному : акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%) 1/4 = 15,8%.
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%) 1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность) (365 / Количество дней владения активом) − 1
(1 + 74%) (365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива) (1 / Количество периодов) − 1
((270 × 20 + 2 × 20) / 200 × 20) (1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как победить выгорание
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Правило трех сигм гласит, что практически все значения нормально распределенной случайной величины лежат в диапазоне трех стандартных отклонений от среднего арифметического значения случайной величины. Случайной величиной у нас выступает годовая доходность по акции
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.
Составление инвестиционного портфеля по Марковицу для чайников
В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.
Введение в портфельную теорию
Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.
Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.
Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.
Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.
wi — доля инструмента в портфеле;
ri — доходность инструмента.
Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).
σi — стандартное отклонение доходностей инструмента;
kij — коэффициент корреляции между I,j-м инструментом;
Vij — ковариация доходностей i-го и j-го финансового инструмента;
n — количество финансовых инструментов в рамках портфеля.
Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.
Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.
Минимизируем риск при минимально допустимом уровне доходности
Максимизируем доходность при заданном уровне риска
Пример расчетов в Excel
Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.
В нашем примере будет использован более простой подход — составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов — платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.
Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.
Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.
Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)
Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)
Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)
Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».
В результате получаем ковариационную матрицу.
Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.
Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23
Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))
Этап 7. Портфель минимального риска.
Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.
При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.
Визуально портфель выглядит так:
Этап 8. Портфель максимальной доходности.
Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp 30
Последние новости
Рекомендованные новости
Рынок США. Неделя будет богатой на события
Индекс МосБиржи теряет еще 3%. Уже ниже 3700 пунктов
40% дивдоходности в российской бумаге в 2022
Ключевые события недели: Центробанки, дивотсечки, экспирация
Несправедливо забытые акции. Подборка №4
Акция, которая приносит по 20% ежегодно уже 40 лет
Инвесторы теряют на акциях Robinhood. Бумаги упали на 47% ниже цены IPO
Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru
* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.
Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.
Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.