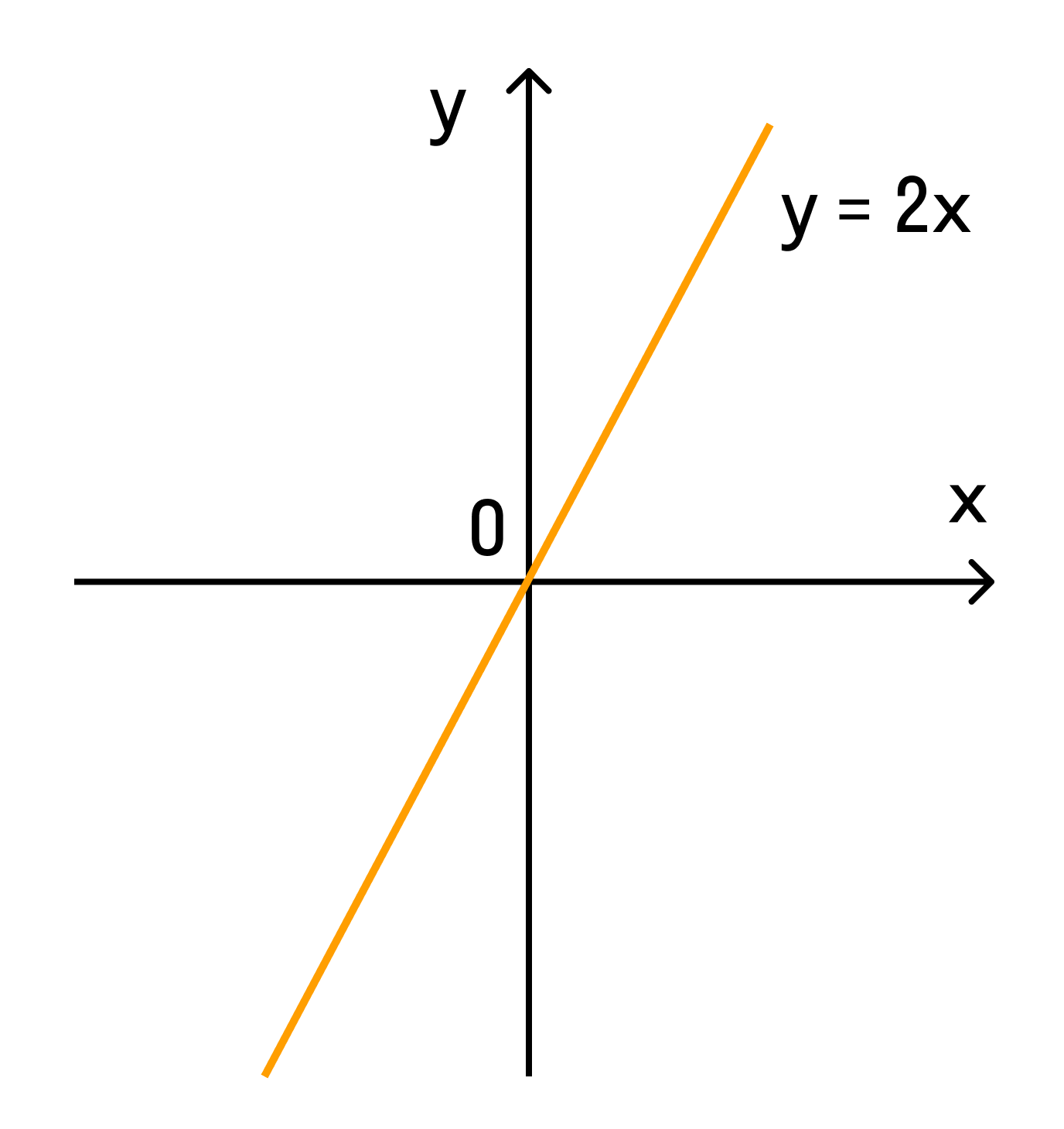Как рассчитать пропорционально сумму
1. Вычисляем, во сколько раз отличается 100 от суммы 150 и 50.
100/(150+50) = 0,5
2. Умножаем наши суммы на полученный к-т.
150 * 0,5 = 75
50 * 0,5 = 25
(3)Формулой это типа:
Ч1 = 150
Ч2 = 100
Ч3 = 50
Сумма = Ч2 / (Ч1 + Ч3)
Ч1 = Ч1 + Ч1 * Сумма
Ч3 = Ч3 + Ч3 * Сумма
Все понятно, всем спасибо.
(20)
declare t table (id int, b decimal)
declare @sum as decimal
insert t values (1, 100), (2, 50)
select
cast(@sum / (SUM(b) OVER()) * b as decimal(15,2)) AS t
from
t
Усложним задачу:
Есть главный документ.
Сумма документа = 150
Нал = 50
БезНал = 100
Он делится на 2 документа.
Это 1с розница, программно деление чека выглядит так:
Если Константы.ДваФР.Получить() Тогда
Запрос = Новый Запрос(»
|ВЫБРАТЬ * ПОМЕСТИТЬ ТабТов ИЗ &ТабТов КАК ТТ;
|ВЫБРАТЬ *
|ИЗ
| ТабТов КАК Товары
|ГДЕ
| Товары.Номенклатура.ТоварОрганизации = &Организация»);
Запрос.УстановитьПараметр(«ТабТов», Товары.Выгрузить());
ВремКассаККМ = КассаККМ;
Оплаты = Оплата.Выгрузить();
Организации = Справочники.Организации.Выбрать();
Пока Организации.Следующий() Цикл
Если Организации.Ссылка = Магазин.ОсновнойСклад.Организация Тогда;
Организация = Справочники.Организации.ПустаяСсылка();
Иначе
Организация = Организации.Ссылка;
КонецЕсли;
Запрос.УстановитьПараметр(«Организация», Организация);
Результат = Запрос.Выполнить();
Если Не Результат.Пустой() Тогда
ЭтотОбъект.Товары.Загрузить(Результат.Выгрузить());
ФР = ПолучитьСерверТО().ПолучитьИдентификаторПоИдКассы(Организация);
Если ЗначениеЗаполнено(Организация) И Не ПустаяСтрока(ФР) Тогда
КассаККМ = ПолучитьСерверТО().ПолучитьКассуККМ(ФР);
Иначе
КассаККМ = ВремКассаККМ;
КонецЕсли;
ИтогСуммы = Товары.Итог(«Сумма»);
ИтогОплат = Оплаты.Итог(«Сумма»);
Если ИтогСуммы <> ИтогОплат Тогда
ЭтотОбъект.Оплата.Загрузить(Оплаты);
Для Каждого ФормаОплат Из Оплата Цикл
КонецЦикла;
КонецЕсли;
ЗавершитьЗакрытиеЧека2(Печать, РучнойРежим, ВыбратьДокументПечати, ФР);
КонецЕсли;
КонецЦикла;
Иначе
ЗавершитьЗакрытиеЧека2(Печать, РучнойРежим, ВыбратьДокументПечати);
КонецЕсли;
Как рассчитать пропорциональную сумму
Проще говоря, пропорциональная сумма представляет собой единое целое, например частичное возмещение оплаченной арендной платы за один месяц. Как правило, чтобы рассчитать пропорциональную сумму для ко
Содержание:
Проще говоря, пропорциональная сумма представляет собой единое целое, например частичное возмещение оплаченной арендной платы за один месяц. Как правило, чтобы рассчитать пропорциональную сумму для конкретной транзакции, разделите или распределите деньги или активы на основе пропорции, указанной в контракте, процента использования или другой согласованной переменной. Пропорциональные расходы распространены как в деловых операциях, так и в личных финансах. Вы можете испытывать некоторую пропорциональную зависимость от транзакций с недвижимостью, расчета коммерческих расходов или контрактов на обслуживание.
Продажа недвижимости
При покупке или продаже недвижимости налоги на недвижимость могут быть пропорционально распределены между покупателем и продавцом, поскольку налоговый счет обычно оплачивается ежегодно или раз в полгода. Например, если продажа происходит в конце марта, налоги на недвижимость пропорционально основаны на налоговых ставках за предыдущий год. В этом примере продавец заплатил бы одну четвертую налога на имущество, представляющую январь, февраль и март. Покупатель оплатит оставшиеся три четверти счета за период с апреля по декабрь.
Отмена страхования
Страховая отрасль использует пропорциональные суммы при расчете, сколько из предоплаченной премии возвращается при отмене полиса. Предположим, что вы меняете компанию по автострахованию через три месяца после предварительной оплаты за шесть месяцев страховки от вашего старого работодателя. Это означает, что вы все равно заплатили за три месяца покрытия по предыдущей политике во время перехода. Ваш бывший страховой провайдер пропорционально премию и вернуть вам деньги. Например, если шесть месяцев покрытия стоят 900 долларов, то ежемесячные расходы составят 150 долларов. В этой ситуации страховой провайдер будет пропорционально распределять сумму и вернет вам 450 долларов за три месяца неиспользованного покрытия.
Бизнес расходы
Владельцам бизнеса может потребоваться рассчитать пропорциональные суммы в расчет налоговых вычетов, Если владелец путешествует по делам и проводит часть времени, занимаясь досугом, расходы должны быть разделены. Возможно, владелец бизнеса проводит три дня в отеле для бизнеса, а затем продлевает свое пребывание еще на один день в качестве отпуска. Счет за отель будет пропорционально распределен, а три четверти заявлены как деловые расходы при подаче налоговых деклараций.
Контракты на обслуживание
В договорах аренды
Договоры аренды, которые требуют, чтобы арендная плата выплачивалась в первый день каждого месяца, могут нуждаться в пропорциональной пропорции, когда арендатор въезжает или выезжает в середине месяца. В этой ситуации ежемесячная сумма аренды делится на 30, чтобы найти стоимость за день. Затем управляющий имуществом взимает или возвращает пропорциональную сумму в зависимости от ситуации.
Пропорциональное деление
Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.
Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.
Деление числа на пропорциональные части
Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.
Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:
Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:
Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.
90 : (1 + 2 + 3) = 90 : 6 = 15;
Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.
Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.
Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:
значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то
Второй способ: обозначим искомые части буквами a, b и c:
Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:
Следовательно, c равно:
Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:
так как 15 + 10 + 8 = 33, то
Деление на части, обратно пропорциональные числам
Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как
Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:
Прямая и обратная пропорциональность
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
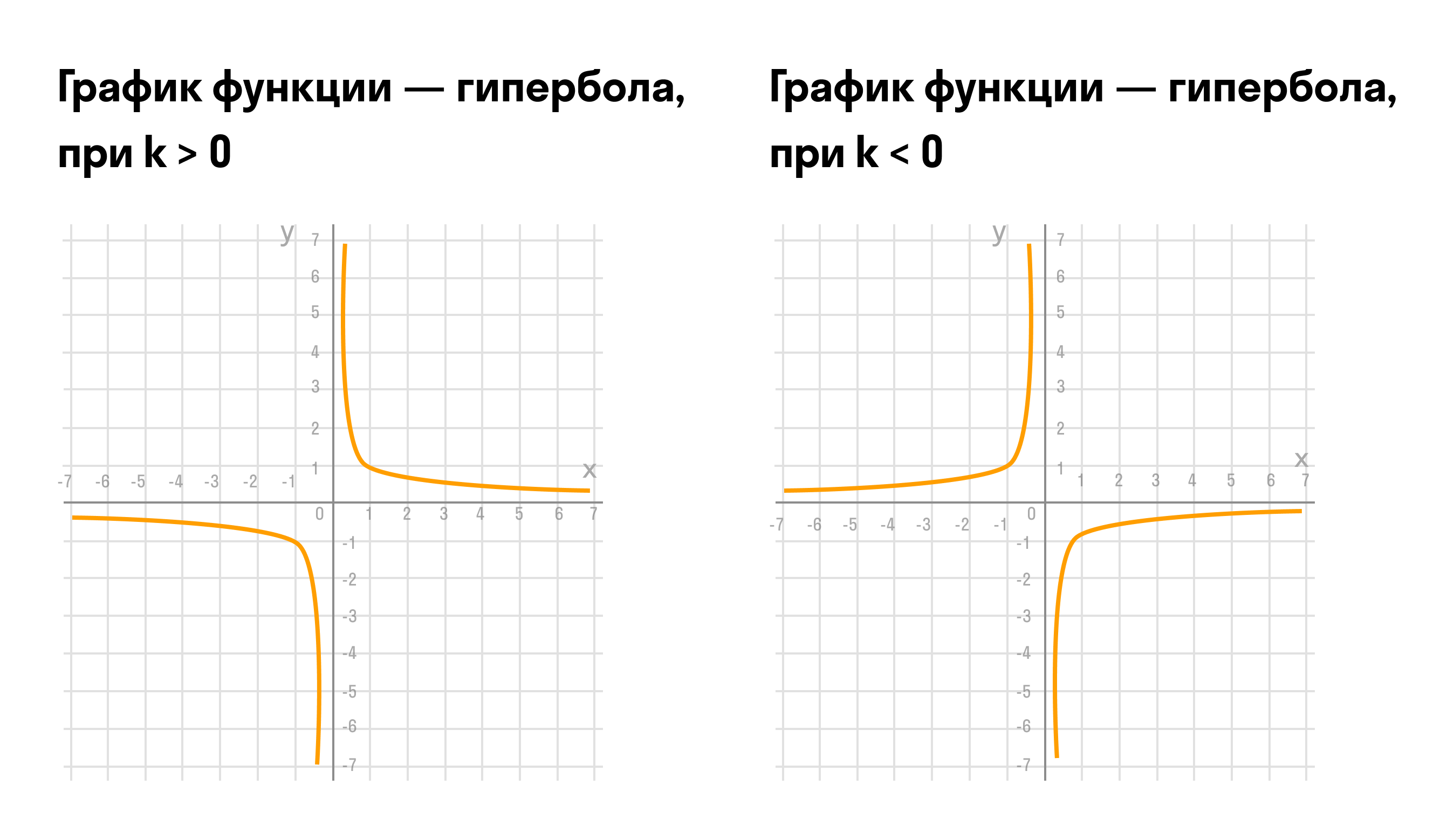
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Соотношения равны, но перевернуты относительно друг друга.
Расчет пропорций при распределении расходов
Если ТРУИП (товары, работы, услуги, имущественные права) используются в облагаемых и не облагаемых налогом на добавленную стоимость операциях, «входной» НДС нельзя принять к вычету в полном объеме, нужно распределить его исходя из пропорции, указанной в п. 4 ст. 170 НК РФ.
Стоимость отгруженных ТРУИП, операции по реализации которых подлежат налогообложению (освобождены от налогообложения) / Общая стоимость отгруженных ТРУИП за налоговый период.
АО производит как облагаемую, так и не облагаемую НДС продукцию. АО начало свою деятельность в январе, за месяц приобрело материалов на сумму 1 200 000 руб. (в т. ч. НДС 20000 руб.). Все материалы оплачены и переданы в производство к 31 марта. 10 % этих материалов было использовано в не облагаемой НДС деятельности, 5 % в облагаемой и не облагаемой и 85 % только в облагаемой.
Продажи за 1-й квартал составили 3 000 000 руб. (без НДС), 200 000 руб. из которых относились к необлагаемой деятельности.
Рассчитать сумму НДС к возмещению и сумму НДС, которая пойдет в расходы 1-го квартала.
Шаг 1. Определим отношение не облагаемой НДС выручки к общей выручке.
200 000 / 3 000 000 = 6,7 %
Шаг 2. На основе пропорции, полученной на шаге 1, распределим общую стоимость товаров и услуг.