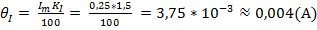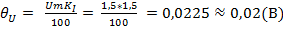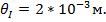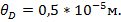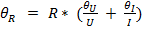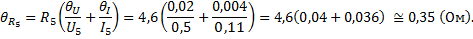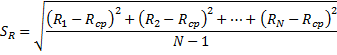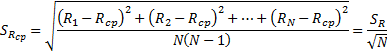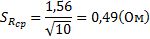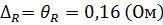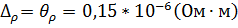Как рассчитать погрешность сопротивления
Вычисление погрешностей.
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
ОПРЕДЕЛЕНИЕ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ
По курсу: ОБЩАЯ ФИЗИКА
СТУДЕНТ ГР. _________________________ _________________________ ________________________
Подпись, дата Инициалы, фамилия
— Ознакомление с методикой обработки результатов измерений
— Определение электрического сопротивления
— Экспериментальная проверка закона Ома
— Определение удельного сопротивления нихрома
— Сравнение двух электрических схем
2. Описание лабораторной установки:
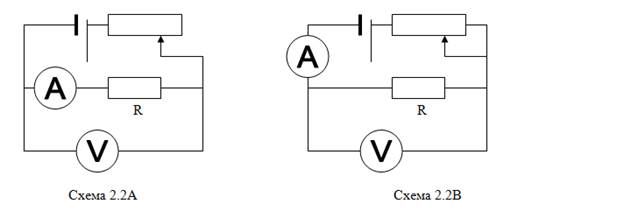
При помощи миллиамперметра, обозначенного символом A, измеряется сила тока в нихромовом проводе. При помощи вольтметра, обозначенного символом V, – падение напряжения на этом проводе. Измерительные приборы можно включить в схему двумя способами, как это показано на двух рисунках. Измеряемое лабораторной работе сопротивление Rуказано на рисунках. Переменный резистор на схемах используется для регулировки силы тока.
Таблица 2.1.
Технические характеристики приборов.
| Прибор | Предел Измерений | Цена Деления | Класс Точности | Систематическая Погрешность | Внутреннее сопротивление |
| Вольтметр | 1,5 В | 0,05 В | 1,5 | 0,02 В | 2500 Ом |
| Миллиамперметр | 250 мА | 5 мА | 1,5 | 4 мА | 0,2 Ом |
| Линейка | 50 см | 1 мм | — | 2 мм | — |
Вычисление электрического сопротивления:
| Закон Ома: | R =  | (1) |
| Для схемы А: | R =  — —  | (2) |
| Для схемы В: | R =  | (3) |
 | (3.4) |
 | (3.5) |
Результаты измерений и вычислений
Таблица 4.1 В
| U, В | 0,3 | 0,35 | 0,4 | 0,45 | 0,5 |
| I, А | 0,07 | 0,075 | 0,09 | 0,1 | 0,11 |
| U/I Ом | 4,3 | 4,7 | 4,5 | 4,5 | 4,5 |
| R Ом | 4,36 | 4,68 | 4,45 | 4,51 | 4,55 |
 | 0,53 | 0,41 | 0,38 | 0,37 | 0,35 |
Таблица 4.2 В
| U, В | 0,1 | 0,15 | 0,2 | 0,25 | 0,3 |
| I, А | 0,07 | 0,1 | 0,13 | 0,16 | 0,19 |
| U/I Ом | 1.42 | 1,5 | 1,53 | 1,56 | 1,58 |
| R Ом | 1,43 | 1,52 | 1,54 | 1,57 | 1,59 |
 | 0,37 | 0,26 | 0,2 | 0,16 | 1,08 |


Примеры вычислений.
| По формуле (1) | R =  = =  = 4,3 (Ом) = 4,3 (Ом) |
| По формуле (2) | R =  — —  = =  — 0,2 = 4,03 (Ом) — 0,2 = 4,03 (Ом) |
| По формуле (3) | R =  = =  = 1,58 (Ом) = 1,58 (Ом) |
| По формуле (4) |  = 3,02(Ом) = 3,02(Ом) |
| По формуле (5) |  0,77 0,77 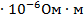 |
Вычисление погрешностей.
6.1 Cистематические погрешности
6.1.1
6.1.2
6.1.3
6.1.4
6.1.5 Вывод формулы для систематической погрешности косвенного измерения электрического сопротивления.
R = R(U,I) =
Вычисления по формуле:

В качестве систематической погрешности итогового результата берем значение, полученное при самом большом токе
6.1.6. Вывод формулы для систематической погрешности удельного сопротивления металла.



Вычисление по выведенной формуле:
6.2 Случайные погрешности.
6.2.1 Средняя квадратичная погрешность отдельного измерения
6.2.2 Среднее квадратичное отклонение
В этой работе проводится измерение неслучайных по своей природе физических величин: электрического сопротивления провода – R и удельного сопротивления нихрома – ρ, поэтому, случайные погрешности определяются только влиянием приборных ошибок на измеряемые величины. В этом случае должны выполняться неравенства SR ≤ θR; SRcp

т.е. полученный результат совпадает с табличным в пределах погрешности.
Лабораторная работа №1
Определение электрического сопротивления
| Студент группы № 1541 | Голубев Н.С. |
| Преподаватель |
| Прибор | Предел Измерений | Цена Деления | Класс Точности | Систематическая Погрешность |
| Вольтметр | 1,5 В | 0,05 В | 1,5 | 0,02 В |
| Миллиамперметр | 250 мА | 5 мА | 1,5 | 4 мА |
| Линейка | 50 см | 1 мм | — | 2 мм |
Электрические сопротивления приборов: 

Как рассчитать погрешность сопротивления
I.Введение
В школьном курсе физики при изучении раздела «Электричество» в ходе выполнения лабораторных работ возникает необходимость в измерении сопротивлений проводников и внутренних сопротивлений источников тока. Для этого используют амперметры и вольтметры из школьного оборудования.
Поскольку измерительные приборы – амперметры и вольтметры не являются идеальными, то встаёт вопрос о выборе схемы соединения приборов, позволяющей с минимальной погрешностью измерить сопротивления проводников и источников тока.
В данной исследовательской работе мы сначала теоретически анализируем погрешности измерений сопротивления проводника при использовании двух схем подключения измерительных приборов, а затем, используя их на практике, рассчитываем погрешности измерений и приходим к выводу о целесообразности использования той или иной схемы. Актуальность данной исследовательской работы заключается в том, что учащиеся могут воспользоваться её результатами при выборе схем во время выполнения лабораторных работ по электричеству. Данную исследовательскую работу можно использовать на уроках физики в качестве обучающего пособия при изучении темы «Электричество» в 8-м, 10-м и при повторении материала, а также при подготовке к ЕГЭ в 11-м классе.
Данную работу можно использовать как методический материал при обучении учащихся подсчёту погрешностей измерений.
При выполнении исследовательской работы автор использовал учебник «Электродинамика» для углублённого изучения физики под редакцией Г.Я. Мякишева, учебник Калашникова «Электричество» и «Физический практикум для классов с углублённым изучением физики» под редакцией Ю.И.Дика и О.Ф.Кабардина.
II.Теоретическая часть
2.1 Из закона Ома для участка цепи электрическое сопротивление проводника можно рассчитать R=U/I.
Для нахождения сопротивления R необходимо измерить приложенное к проводнику напряжение U и силу тока I в проводнике при этом напряжении.
Напряжение измеряется с помощью вольтметра, сила тока измеряется с помощью амперметра
Вольтметр включается параллельно участку цепи, на котором измеряется напряжение. Это напряжение Uиз равно показанию вольтметра.
Амперметр включается последовательно к участку цепи, в котором измеряется сила тока. Эта сила тока Iиз равна показанию амперметра.
Для измерения сопротивления проводника приведём две возможные электрические схемы соединения вольтметра V, амперметра A и исследуемого проводника (сопротивления) Rx.
Схема №1. На 1-ой схеме проводник и амперметр соединены последовательно.
Вольтметр измеряет и показывает сумму напряжения на проводнике Uх и напряжения на амперметре UА.
Амперметр измеряет и показывает силу тока IА, которая равна силе тока в проводнике Ix:IА = Ix
Из закона Ома R х = Uх / Iиз
Напряжение на амперметре UА согласно закону Ома равноUА=IАRА=Iиз RА. Напряжение на проводнике равно разности между напряжением на вольтметре и напряжением на амперметре U х =U из–Iиз RА.
Тогда R х = Uх / Iиз = (U из–Iиз RА) : Iиз. Окончательно получаем R х = U из/ Iиз – RА.
Отношение U из/ Iиз является общим сопротивлением последовательно соединенных проводника и амперметра (сопротивлением, определенным по показаниям приборов):
Поэтому сопротивление проводника будет равно:R х = R из – R А
Это выражение следует из формулы общего сопротивления при последовательном соединении проводников
Отсюда следует, что ΔR =R из – R х = RА
Сопротивление Rиз, вычисленное по показаниям амперметра и
вольтметра по схеме №1, отличается от сопротивления проводника Rx на величину сопротивления амперметра. Сопротивление школьного амперметра по нашим измерениям не превышаетRА = 0,1 Ом
Относительное изменение сопротивления проводника Rx от сопротивления Rиз, определенного по показаниям амперметра и вольтметра, то есть относительная погрешность измерения равна:
2.2 На схеме 2 проводник и вольтметр соединены параллельно.
Амперметр измеряет и показывает сумму сил токов через проводник Jx и через вольтметр Jv :Jиз = Jx + Jv
Вольтметр измеряет и показывает напряжение на проводнике: Uиз = Ux.
Из закона Ома сопротивление проводникаRх = Uх / Iх = Uиз / Iх
Сила тока через вольтметр Iv согласно закону Ома Iv = Uv / Rv =Uиз / Rv
Сопротивление Rиз = Uиз / Iиз , т.е. определенное по показателям приборов, в этом случае является общим сопротивлением параллельно соединенных проводника и вольтметра. Поэтому сопротивление проводника будет равно
(Это выражение следует и из формулы общего сопротивления при параллельном соединении проводников).
Сопротивление Rиз, вычисленное по показаниям амперметра и вольтметра, отличатся от сопротивления проводника Rx в этом случае на величину ∆R = Rx – Rиз =Rх: (1 + Rv / Rx)
Относительное отличие сопротивления проводника Rx от сопротивления Rиз, определенного по показаниям амперметра и вольтметра, то есть относительная погрешность измерения равна: ε = ∆R / Rx = Rx : (Rv + Rx)
Видно, что отличие значения сопротивления Rиз, полученного на основе экспериментальных данных от истинного значения Rx тем меньше, чем больше сопротивление вольтметра Rv и чем меньше сопротивление проводника Rx.
Проведённые нами измерения сопротивления школьного вольтметра дали результат
Rv = 800 Ом.
Током через вольтметр Iv можно пренебречь, если собственное сопротивление RV велико по сравнению с сопротивлением резистора: RV >> RX.
Допустимость использования выражения Rиз = Uиз / Iиз легко проверить на опыте: если при отключении вольтметра в схеме №2 показания амперметра не изменятся, то влиянием вольтметра можно пренебречь.
Если при отключении вольтметра показания амперметра существенно меняются, то необходимо учесть сопротивление вольтметра. Обычно оно указано на шкале прибора или в его паспорте. На школьных вольтметрах Лаборатории L – микро такой информации нет.
Мы определяли сопротивление вольтметра опытным путём, используя электрическую схему №4
Измерив значения Iv и Uv в этой цепи, мы рассчитали Rv:
III. Практическая (исследовательская) часть
3.1 Собрали электрическую цепь по схеме №1.
Rиз1 = U из/ Iиз = 4,60В/0,42А= 11,00 Ом
R х1 = R из1 – R А = 11,00 Ом – 0,10 Ом = 10,90 Ом
Rиз2 = U из/ Iиз = 3,90В/0,58А= 6,70 Ом
R х2 = R из2 – R А = 6,70 Ом – 0,10 Ом = 6,60 Ом
3.2 Значения измеренных и расчётных величин внесли в таблицу.
Rиз1 = Uиз / Iиз = 4,0В/0,37А=10,80 Ом
Rиз2 = Uиз / Iиз = 4.3В/0,70А=6,14 Ом
3.4 Значения измеренных и расчётных величин внесли в таблицу.
Погрешности измерения сопротивлений.
ОСНОВЫ ТЕОРИИ
Закон Ома для однородного участка цепи.

Величина U = I×R называется падением напряжения на проводнике и численно равна количеству тепла, выделяющегося в проводнике при прохождении через него единичного электрического заряда.
Для однородного участка (т.е. не содержащего э.д.с.) разность потенциалов на концах участка численно равна падению напряжения на этом участке, т.е. Dj= U.
Если обычный аналоговый вольтметр (отклонение стрелки которого обусловлено током, проходящим в рамке или катушке) присоединить к точкам 1 и 2 участка цепи, то он покажет разность потенциалов Dj между этими точками. Разность потенциалов в этом случае будет равна падению напряжения U на вольтметре, т.е.

Сопротивление проводников.
Если участок цепи представляет собой проводник длиной l постоянного сечения S, однородного химического состава, то сопротивление R этого проводника определяется по формуле:

где r- удельное сопротивление материала.
При комнатной температуре наименьшее удельное сопротивление имеют проводники из химически чистых металлов. Удельное сопротивление сплавов имеет большую величину, что позволяет применять их для изготовления резисторов с большим сопротивлением (реостаты, нагревательные элементы, шунты и добавочные сопротивления). В табл. 1 даны значения удельного сопротивления некоторых материалов.
| Металл или сплавы (состав %) | Удельное сопротивление при 20°С (Ом×мм 2 /м) |
| Серебро | 0,016 |
| Медь | 0,017 |
| Алюминий | 0,028 |
| Железо | 0,093 |
| Константан (58,8% Cu, 40% N, 1,2% Mn) | 0,44-0,52 |
| Нихром | 1,0-1,1 |
| Графит | 8,0 |
Методы измерения сопротивления.
Одним из методов измерения сопротивления проводника является метод «амперметра-вольтметра», состоящим в практическом использовании закона Ома для однородного участка цепи. Из формул (1) и (2) следует

т.е. измеряя разность потенциалов U на концах проводника и величину тока I, протекающего через него, можно определить сопротивление R проводника.
Другим методом измерения сопротивлений является метод мостовых схем, который рассматривается в другой лабораторной работе. В мостовых схемах не требуется измерять токи и напряжения, поэтому они дают более точные результаты.
Погрешности измерения сопротивлений.
При измерениях возникают погрешности, имеющие различную природу. Погрешность метода (или теоретическая погрешность) связана с несовершенством метода, с упрощениями, принятыми в уравнениях для измерений. Погрешность метода проявляется, прежде всего, как систематическая, для компенсации которой возможно введение поправок. При измерении сопротивления методом «амперметра-вольтметра» возникает погрешность, определяемая способом подключения амперметра и вольтметра к исследуемому участку цепи.
Для измерения сопротивления R вольтметр и амперметр могут быть включены в цепь по одной из схем, изображенных на рис.1

 |
а б
Расчет по формуле (4) будет содержать систематическую погрешность, обусловленную особенностями метода (упрощениями, принятыми при таком расчете).
Величина истинного сопротивления R проводника будет равна

где через U обозначена разность потенциалов на участке 1-2.
Следовательно, разница DR между результатами измерения сопротивления RЭ по формуле (4) и истинным R и является той методической ошибкой, которая возникает при данном способе включения измерительных приборов.

Относительная погрешность этого метода равна:

Т.е. точность измерения сопротивления будет тем больше, чем меньше сопротивление RA амперметра по сравнению с сопротивлением R проводника. (Идеальным будет амперметр с бесконечно малым собственным сопротивлением).
Тогда по закону Ома (1):


Так как измеряемый ток равен I = IR + IV то, учитывая (9), получим
Величина истинного сопротивления R проводника будет равна


Следовательно, в этом способе измерения также возникает погрешность метода
Относительная погрешность этого метода равна:

т.е. точность измерения сопротивления будет тем больше, чем больше сопротивление вольтметра по сравнению с сопротивлением R проводника Идеальным будет вольтметр с бесконечно большим собственным сопротивлением. Высокоомными являются электронные аналоговые и цифровые вольтметры, вносящие малую погрешность.
Другим источником погрешности являются инструментальные погрешности, обусловленные конструкцией прибора. Инструментальные погрешности содержат как систематическую, так и случайную составляющую. При каждом отдельном измерении сопротивления R мы производим измерения тока I и разности потенциалов U с погрешностью, определяемой классом точности измерительного прибора
где gA— класс точности амперметра, имеющего предельный ток Im,
Погрешность определения сопротивления, обусловленная погрешностями приборов определяется по правилам переноса погрешностей косвенных измерений

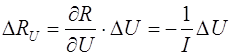


Из формул (13)-(13′) видно, что приборную погрешность можно уменьшить, применяя амперметр и вольтметр высокого класса точности, а также выбирать токи и напряжения такой величины, чтобы стрелки приборов при снятии показаний находились во второй половине шкалы (возможно ближе к пределу измерений).
Случайные погрешности возникают при сочетании не воспроизводимых от измерения к измерению факторов: нестабильности источника тока, погрешности оператора, случайной составляющей приборной погрешности и т.д. Для определения случайной погрешности проводят серию многократных измерений Ri при разных токах и напряжениях. Статистическая погрешность DRСТ определяется в соответствии с правилами обработки многократных измерений.
Полная погрешность определяется композицией приборной DRПР и статистической DRСТ погрешностей


ОПИСАНИЕ УСТАНОВКИ
Прибор FRM-01 представлен на рис.2. К основанию (1) прикреплена колонна (2) с нанесенной миллиметровой шкалой (3). На колонне укреплены два неподвижных кронштейна (4) и один подвижный кронштейн (5), который может передвигаться вдоль колонны и фиксироваться в любом положении. Между верхним и нижним кронштейном натянут нихромовый провод (6).
 |
Рис. 2
Через контактный зажим на подвижном кронштейне обеспечивается хорошее гальваническое соединение с проводом. На подвижном кронштейне нанесена черта, которая облегчает определение по шкале длины отрезка измеряемого нихромового провода. Нижний, верхний и центральный подвижный контакты нихромового провода подведены при помощи проводов низкого сопротивления к измерительной части прибора (7), которая помещена в центральном корпусе.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Заготовьте таблицу результатов измерений.
2. Ручку регулятора тока установите в положение минимального тока (поверните против часовой стрелки до упора). Передвигая подвижный кронштейн (5), установите произвольную длину l проводника. Определите длину проводника, его диаметр (микрометром), класс точности приборов и запишите результаты в табл. 3
3. Включите установку и произведите пять измерений сопротивления при разных токах методом точного измерения тока
4. Заготовьте таблицу, аналогичную табл. 2. Произведите аналогичную серию измерений методом с точным измерением напряжения
5. Выключите установку.
ОБРАБОТКА РЕЗУЛЬТАТОВ
1. Вычислите неисправленное RЭi и исправленное значения Ri сопротивления проводника по формулам (4), (6) и (10), а также их средние значения и в каждом методе измерения.
2. Определите погрешности метода em1 и em2 по формулам (8)и (11) для каждого метода измерения.
3. Определите приборные погрешности DRПР и eR для двух опытов по формулам (12)-(13′) (для минимального и максимального тока), используя данные более точного метода.
4. Определите случайную погрешность DRСТ и eСТ (для более точного метода).
5. Определите полную абсолютную и относительную погрешности измерения сопротивления DR и eR по формулам (14) и (14′).
6. Определите удельное сопротивление r нихромового провода по формуле (3).
7. Выведите формулу для определения погрешности по правилам оценки погрешностей косвенных измерений (через погрешности DR, Dd, и Dl). Определите абсолютную и относительную Dr погрешности для наиболее точного результата измерений .
ВЫВОДЫ
1. Запишите результат измерения R и r в стандартной форме.
2. Какой метод измерения сопротивления точнее? Подтвердите это сравнением погрешностей обоих методов включения амперметра и вольтметра.
3. Какой вид погрешности (метода, приборная или статистическая) имеет наибольшее влияние на результат определения погрешности сопротивления в Ваших опытах?
4. Следует ли учитывать сопротивления амперметра и вольтметра в данных опытах?
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Дайте определение разности потенциалов и падения напряжения на участке цепи. В каком случае они равны?
2. Каков физический смысл сопротивления проводника? От чего оно зависит?
3. В чем состоит метод измерения сопротивления с точным измерением тока? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить?
4. В чем состоит метод измерения сопротивления с точным измерением напряжения? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить?
5. Как определяются приборные и случайные погрешности измерения в данной работе?
ЛИТЕРАТУРА: [1: 34]; [2: 9.1, 9.2]; [3: 98].