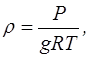Как рассчитать погрешность скорости

Погрешности указателей скорости

Инструментальные погрешности ΔV_и возникают из-за несовершенства конструкции прибора и неточности его регулировки. Каждый экземпляр прибора имеет свои значения инструментальных погрешностей.

Аэродинамические погрешности ΔV_a возникают из-за искажения воздушного потока в месте установки приемника воздушного давления. Характер и величина этих погрешностей зависят от типа воздушного судна, места установки приемника воздушного давления, скорости и высоты полета, конфигурации ВС. На скоростных самолетах они могут достигать нескольких десятков километров в час.

Аэродинамические погрешности одинаковы для всех ВС данного типа. Они определяются при проведении летных испытаний, публикуются в руководстве по летной эксплуатации ВС и заносятся в специальный график или таблицу поправок. На некоторых типах воздушных судов для упрощения учета поправок указателя скорости составляются таблицы суммарных поправок ΔV_Σ, учитывающие как инструментальные, так и аэродинамические погрешности.

В общем случае указатель скорости имеет два вида методических погрешностей, то есть погрешностей, вызванных самим методом измерения, несоответствием условий, принятых при расчете шкал приборов, фактическому состоянию атмосферы. Это погрешность за счет изменения сжимаемости воздуха и методическая погрешность из-за изменения плотности воздуха.

Погрешность из-за изменения сжимаемости вызвана тем, что при полете на скоростях более 350…400 км/ч воздух перед ПВД сжимается, и его плотность увеличивается. Это вызывает увеличение скоростного напора и, следовательно, завышение показаний указателя скорости.

Эти погрешности не могут быть учтены заранее при тарировке шкалы однострелочного указателя скорости, так как сжимаемость воздуха зависит не только от скорости полета, но и от плотности воздуха. Но однострелочные указатели рассчитаны на небольшие скорости и высоты полета, на которых данная погрешность не превышает единиц километров в час, то есть меньше цены деления на шкале указателя, поэтому для однострелочных указателей погрешность из-за изменения сжимаемости несущественна и на практике не учитывается.

В комбинированных указателях скорости показания широкой стрелки отградуированы по формуле (7.5), которая выведена уже с учетом сжимаемости воздуха. Но все равно она оказывается учтенной не полностью. Поскольку при градуировке в формулу подставлены P₀ и T₀, получается, что сжимаемость учитывается правильно только при полетах в условиях стандартной атмосферы у земли. С увеличением же высоты на самом деле сжимаемость изменяется, вследствие чего и возникает погрешность, поэтому данный вид погрешности и называется правильно «из-за изменения» сжимаемости.

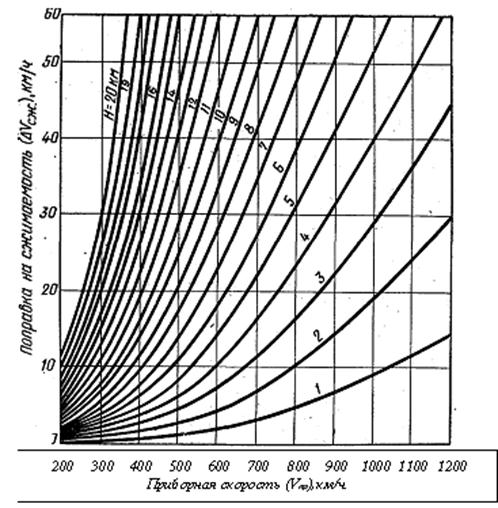
На рис.7.7 показан график зависимости поправки на изменение сжимаемости от высоты и скорости полета.

Рис. 7.7. Поправка на изменение сжимаемости воздуха

Из-за неучета сжимаемости указатель скорости всегда показывает скорость больше фактической. Это означает, что поправка на изменение сжимаемости всегда отрицательна.

На практике для учета этой поправки используется таблица. Поскольку погрешность является методической, то данная таблица является единой для всех типов ВС и указателей скорости. При ее использовании необходимо помнить, что все значения поправок в таблице на самом деле являются отрицательными. Просто знак «минус» для экономии места в таблице не указан.

При формировании показаний узкой стрелки КУС с помощью анероидной коробки измеряется статическое давление, что позволяет при градуировке прибора учесть и изменение сжимаемости с высотой, поэтому при расчете истинной скорости по показаниям узкой стрелки поправку на изменение сжимаемости не учитывают.

Поскольку узкая и широкая стрелки КУС отградуированы по-разному, то есть для разных расчетных значений плотности, то и методическая погрешность в их показаниях будет различной.

Можно показать, что по показаниям узкой стрелки истинную воздушную скорость V_и можно рассчитать по формуле:

(7.6)

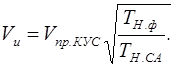
В данной формуле под V_пр.КУС понимаются показания узкой стрелки с уже учтенными инструментальными и аэродинамическими поправками, то есть в предположении, что они равны нулю.

Из данной формулы можно видеть, что при одном и том же показании узкой стрелки V_пр.КУС, чем выше фактическая температура, тем больше истинная скорость. То есть, при повышенных температурах прибор занижает показания, показывает скорость меньше правильной, и наоборот.

Разность между V_и и V_пр.КУС и является методической температурной поправкой. На практике значение самой этой поправки (разности скоростей) обычно не рассчитывается, а просто по V_пр.КУС сразу рассчитывают истинную скорость, то есть уже с учетом методической поправки. Расчет может быть произведен на НЛ-10М или по формуле (7.6).

Учесть методическую поправку по показаниям широкой можно с помощью следующего соотношения:

(7.7)

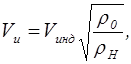
где ρ_H – фактическая плотность воздуха на уровне полета,

V_инд – так называемая индикаторная скорость, полученная путем прибавления к приборной скорости V_пр инструментальной, аэродинамической поправок и поправки на изменение сжимаемости.

Плотность воздуха можно выразить через температуру и давление с помощью формулы

поэтому формулу (7.7) можно записать и в таком виде:

(7.8)

Источник

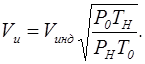
Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник

Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 6%. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1%.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Источник

Расчет погрешности измерений

3.1 Среднеарифметическая погрешность.Как уже отмечалось раньше, измерения принципиально не могут быть абсолютно точными. Поэтому в ходе измерения возникает задача об определении интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Такой интервал указывают в виде абсолютной ошибки измерения.

Если предположить, что грубые промахи в измерениях устранены, а систематические ошибки сведены к минимуму тщательной настройкой приборов и всей установки и не являются определяющими, то результаты измерений будут, в основном, содержать только случайные погрешности, которые являются знакопеременными величинами. Поэтому, если проведено несколько повторных измерений одной и той же величины, то наиболее вероятным значением измеряемой величины является ее среднеарифметическое значение:

(1)

Погрешностью или абсолютной ошибкой отдельного измерения называют разность между значением, полученным в данном измерении, и среднеарифметическим значением измеряемой величины:

(2)

Средней абсолютной ошибкойназывается среднеарифметическое модулей абсолютных ошибок отдельных измерений:

(3)

При достаточно большом числе измерений случайные ошибки возникают с равной вероятностью как в сторону увеличения, так и в сторону уменьшения измеряемой величины, то есть можно считать, что истинное значение измеряемой величины заключено в интервале

(4)

Последнее неравенство обычно принято записывать как окончательный результат измерения следующим образом:

(5)

Относительная погрешность.Абсолютная ошибка определяет интервал наиболее вероятных значений измеряемой величины, но не характеризует степень точности произведенных измерений. Например, расстояние между населенными пунктами, измеренное с точностью до нескольких метров, можно отнести к весьма точным измерениям, в то время как измерение диаметра проволоки с точностью до 1 мм, в большинстве случаев будет являться весьма приближенным измерением.

Степень точности проведенных измерений характеризует относительная погрешность.

Средней относительной погрешностьюили просто относительной ошибкой измерения называется отношение средней абсолютной ошибки измерения к среднему значению измеряемой величины:

(6)

или выраженная в процентах

(7)

Относительная ошибка является безразмерной величиной и обычно выражается в процентах.

3.2 Погрешность метода или приборная погрешность.Среднеарифметическое значение измеряемой величины тем ближе к истинному, чем больше проведено измерений, при этом абсолютная погрешность измерения с увеличением их числа стремится к значению, которое определяется методом измерения и техническими характеристиками используемых приборов.

Погрешность методаили приборную погрешность можно рассчитать по одноразовому измерению, зная класс точности прибора или другие данные технического паспорта прибора, в котором указывается либо класс точности прибора, либо его абсолютная или относительная погрешность измерения.

Класс точностиприбора выражает в процентах номинальную относительную ошибку прибора, то есть относительную ошибку измерения, когда измеряемая величина равна предельному для данного прибора значению

(8)

Класс точности указывается на шкале прибора цифрой, обведенной кружочком. Согласно ГОСТу все электроизмерительные приборы разделяются на 8 классов: 0,05; 0,1; 0,2; 0,5; 1.0 1,5; 2,5; 4,0.

Абсолютная погрешность прибора равна предельному для данного прибора значению измеряемой величины, умноженному на класс точности (К) и разделен­ному на 100:

(9)

Абсолютная погрешность прибора не зависит от значения измеряемой величины.

Относительная погрешность прибора (по определению):

(10)

При работе с простыми приборами (линейка, мензурка и т.п.), классы точности и погрешности которых не определены техническими характеристиками, абсолютную погрешность прямых измерений принимают равной половине цены деления данного прибора. (Ценой деления называют значение измеряемой величины при показаниях прибора в одно деление).

Приборную погрешность косвенных измеренийможно рассчитать, используя правила приближенных вычислений. В основе вычисления погрешности косвенных измерений лежат два условия (предположения):

1. Абсолютные ошибки измерений всегда очень малы по сравнению с измеряемыми величинами. Поэтому абсолютные ошибки (в теории) можно рассматривать как бесконечно малые приращения измеряемых величин, и они могут быть заменены соответствующими дифференциалами.

2. Если физическая величина, которую определяют косвенным путем, является функцией одной или нескольких непосредственно измеряемых величин, то абсолютная ошибка функции, обусловленная бесконечно малыми приращениями, является также бесконечно малой величиной.

При указанных допущениях абсолютную и относительную погрешность можно рассчитать, используя известные выражения из теории дифференциального исчисления функций многих переменных:

	(11)
	(12)

	(13)
	(14)

Таким образом: а) абсолютная ошибка косвенного метода измерения равна сумме модулей произведений частных производных функции измерения и соответствующих абсолютных ошибок прямых измерений; б) относительная ошибка косвенного метода измерения равна сумме модулей дифференциалов от логарифма натурального функции измерения, определяемой расчетной формулой.

Выражения (13) и (14) позволяют рассчитать абсолютные и относительные погрешности по одноразовому измерению. Заметим, что для сокращения расчетов по указанным формулам достаточно рассчитать одну из погрешностей (абсолютную или относительную), а другую рассчитать, используя простую связь между ними:

(15)

На практике чаще пользуются формулой (13), так как при логарифмировании расчетной формулы произведения различных величин преобразуются в соответствующие суммы, а степенные и показательные функции преобразуются в произведения, что намного упрощает процесс дифференцирования.

Для практического руководства по расчету погрешности косвенного метода измерения можно пользоваться следующим правилом:

Чтобы вычислить относительную ошибку косвенного метода измерения, нужно:

1. Определить абсолютные ошибки (приборные или средние) прямых измерений.

2. Прологарифмировать расчетную (рабочую) формулу.

3. Принимая величины прямых измерений за независимые переменные, найти полный дифференциал от полученного выражения.

4. Сложить все частные дифференциалы по абсолютной величине, заменив в них дифференциалы переменных соответствующими абсолютными ошибками прямых измерений.

5. Используя полученное выражение, рассчитать относительную погрешность.

6. По формуле (15) рассчитать абсолютную ошибку.

Например, плотность тела цилиндрической формы вычисляется по формуле:

(16)

Получим формулу для расчета погрешностей.

1. Исходя из используемого оборудования, определяем абсолютные погрешности измерения массы, диаметра и высоты цилиндра (∆m, ∆D, ∆h соответственно).

2. Логарифмируем выражение (16):

4. Заменяя дифференциал независимых переменных на абсолютные ошибки и складывая модули частных приращений, получаем:

5. Используя численные значения m, D, h, D, m, h, рассчитываем Е.

6. Вычисляем абсолютную ошибку

где r рассчитано по формуле (16).

Предлагаем самим убедиться, что в случае полого цилиндра или трубки с внутренним диаметром D₁ и внешним диаметром D₂

К расчету ошибки метода измерения (прямого или косвенного) приходится прибегать в случаях, когда многократные измерения либо невозможно провести в одних и тех же условиях, либо они занимают много времени.

Если определение погрешности измерения является принципиальной задачей, то обычно измерения проводят многократно и вычисляют и среднеарифметическую погрешность и погрешность метода (приборную погрешность). В окончательном результате указывают большую из них.

О точности вычислений

Ошибка результата определяется не только неточностями измерений но и неточностями вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого вспомним правила математического действия с приближёнными числами.

Правила округления чисел

При округлении оставляют лишь верные знаки, остальные отбрасываются.

1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.

2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля.

Например, различные округления числа 35,856 будут: 35,9; 36.

3. Если отбрасываемая цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее чётное число, то есть, последняя сохраняемая цифра остаётся неизменной, если она чётная и увеличивается на единицу, если она нечётная.

Например, 0,435 округляем до 0,44; 0,365 округляем до 0,36.

Источник