Как рассчитать погрешность амперметра

Амперметр и вольтметр. Правила включения.

теория по физике 🧲 постоянный ток

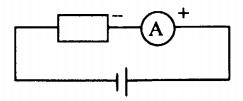
Для измерения силы тока используется амперметр. В идеале собственное сопротивление амперметра стремится к нулю, и оно никак не влияет на значение силы тока. Он включается в цепь последовательно с соблюдением полярности:

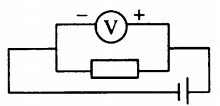
Для измерения напряжения участка цепи используется вольтметр. В идеале собственное сопротивление вольтметра стремится к бесконечности, и устройство не проводит через себя ток. Он включается в электрическую цепь параллельно участку, в котором будет измеряться напряжение, с соблюдением полярности:

Как правильно записывать показания измерительных приборов с учетом погрешности

При записи величин (с учетом погрешности) следует пользоваться формулой:

где A — измеряемая величина, a — результат измерений, Δa — погрешность измерений.

Погрешность измерений равна половине цены деления шкалы измерительного прибора, если в задаче не указана другая величина погрешности.

Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы. Чтобы найти цену деления шкалы, нужно:

Пример №1. Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.

Видно, что стрелка вольтметра встала на значении «2,0» Вольт. Она немного не дотягивает до штриха «2», но к нему она находится ближе, чем к предыдущему штриху.

Два ближайших штриха шкалы с указанными значениями имеют значения 1 и 2 В. Всего между ними 5 промежутков. Следовательно, цена деления шкалы равна: (2 – 1)/5 = 0,2 (Вольт).

Так как по условию задачи погрешность равна половине цене деления шкалы, то она равна 0,1 Вольтам. Следовательно, вольтметр показывает: 2,0 ± 0,1 В.

Источник

Погрешности измерений

Общие сведения об измерениях. Погрешности измерений и средств измерений

Общие сведения об измерениях

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.

Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.

Погрешности измерений

Погрешность является одной из основных характеристик средств измерений.

Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.

Абсолютная погрешность Δ_a прибора есть разность между показанием прибора а_х и истинным значением а измеряемой величины, т.е.

Абсолютная погрешность, взятая с обратным знаком, называется поправкой.

Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна

Приведенная погрешность γ_П есть выраженное в процентах отношение абсолютной погрешности Δ_a к нормирующему значению а_пр

Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).

Погрешности средств измерений

Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.

Класс точности прибора (например, амперметра) дается выражением

При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.

По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:

В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:

(α = 0) 1; 1,5; 2; 2,5; 4; 5; 6;

(α = 1) 10; 15; 20; 25; 40; 50; 60.

Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.

Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.

Примеры решения задач

Задача №1

Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.

Решение

Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)

постоянна и равна классу точности прибора.

Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)

уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.

Абсолютная погрешность однократного измерения

постоянна на всех отметках рабочей части шкалы прибора.

По условию задачи: U_изм = U_i = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; U_пр = 30 В – предел шкалы вольтметра.

Источник

Что такое класс точности амперметра

Ни один прибор в мире не является точным. Величина, которую он измеряет, всегда будет отличаться от истины на ту величину, которую еще называют его погрешностью. Данная погрешность и будет определять класс точности амперметра. Задачей всех производителей измерительной техники, заключается в том, чтобы эта погрешность была, как можно ниже и стремилась к нулю.

Погрешность амперметра устанавливается в результате поверки и сравнении показаний замеров одних и тех же величин с эталонным или образцовым прибором, имеющий более высокий класс точности. При этом значение, полученное на образцовом приборе, считаются действительными.

Что такое амперметр и какие величины он измеряет

Важно! В электроцепь амперметр включают последовательно, а для повышения границы измерений, используют специальные устройства: трансформаторы, шунты м магнитные усилители.

Поскольку ток в цепи напрямую зависит от величины сопротивления [R] элементов электроцепи, то собственное сопротивление прибора [Rа] должно быть предельно низким, стремится к нулю. Это приведет к уменьшению влияния устройства в процессе замеров тока в цепи, тем самым будет повышена точность измерения.

Разновидности амперметров

Они могут быть электромеханическими или аналоговыми, цифровыми или электронными. Базовый набор, как правило, состоит из детектора, передающего устройства и индикатора, самописца или запоминающего устройства.

Аналоговые устройства — самые старые из используемых инструментов. Хотя они надежны для статических и стабильных измерений, они не подходят для динамических и переходных условий. Кроме того, они довольно громоздкие и имеют ограничения из-за использования стрелочной индикации.

Электронные инструменты реагируют быстрее и способны мгновенно обнаруживать динамические изменения тока в сети. Примером является цифровой мультиметр, который способен измерить значения тока в динамическом или переходном режиме за секунды.

Виды погрешностей амперметра

Чтобы понять размер погрешности в измерениях, нужно сравнить полученные результаты с эталонными.

В метрологии используют для всех электротехнических измерителей, как для амперметров, так и для вольтметров, несколько видов погрешностей: абсолютную, относительную и приведенную.

Абсолютная погрешность амперметра — это разность Δ между результатом измерения, полученного на шкале прибора (Xи) и действительным значением силы тока в цепи (Xд). Абсолютная погрешность амперметра описывается простой формулой и выражается в единицах тока А.

Относительная погрешность (δ) — отношение абсолютной погрешности амперметра Δх к действительному показанию силы тока, принимаемому по образцовому прибору. Оно может быть указано как в процентах, тогда частное умножается на 100, либо выражаться в относительных единицах.

Приведенная погрешность — это значение приведенное к диапазону измерения амперметра, приравненного к его шкале. Его получают в виде частного от абсолютной погрешности Δх и нормируемого значения (Xн), в значениях соответствующим абсолютной погрешности Δх умноженной на 100 %:

Класс точности

Это основная характеристика амперметра, которая согласно еще советскому действующему ГОСТ 1845-59, определяет границы возможных погрешностей.

Для всех электроизмерительных приборов, к которым он относится, класс точности (Кл) обозначается в числовом виде по значению, соответствующему предельной допустимой приведенной погрешности δпр, в %.

Все электрические амперметры подразделяются по точности на 8 классов, а затем по группам, которые является важным признаком их классификации:

Обратить внимание! Все приборы, у которых погрешность превышает 4%, являются внеклассными.

Образцовые применяют в электроизмерительных процессах для определения класса точности технических и лабораторных амперметров. Лабораторные применяются в научно-технических процессах при электротехнических исследованиях контроля ведения режимов, например на котельных, ГЭС, ТЭЦ и АЭС.

Важно! На панели амперметра класс точности указывается в кружках, квадратах и звездочках. Если он имеет неравномерную шкалу измерения, Кл обозначается ломаной линией.

Как определить класс точности

Согласно действующих государственных норм, производители амперметров обязаны гарантировать его относительную погрешность измерения, полученную по классу точности, указанной на измерительной панели и в паспорте на прибор. Кроме того, все измерительные приборы должны проходить периодическую поверку в метрологических центрах, на соответствие заводскому классу точности. Если такую аттестацию он не проходит, то не может использоваться в измерительных процессах.

Зная абсолютную погрешность и показание силы тока на шкале, можно просто получить реальную силу тока, действующую в цепи. При этом шкала для применения абсолютной погрешности считается равномерной.

Важно! При выборе шкалы стрелочного амперметра, нужно чтобы рабочее значение тока находилось, примерно, в 2/3 диапазона шкалы. Если стрелка будет находиться практически на 0 или на максимальном показатели шкалы, то относительная погрешность будет очень высокой, то есть доверять таким показаниям не рекомендуется.

Пример нахождения показания амперметра по приведенной погрешности

Для примера рассматривается аналоговый измеритель со шкалой до 25 А.

На шкале имеется обозначение класса точности 2.5, кружок или квадрат отсутствует, поэтому эта погрешность приведенная.

При Хп= 25А и значении p = 2.5 можно рассчитать абсолютную погрешность:

Если пользователь обнаружит на панели класс точности заключенный в квадрат, то погрешность нужно будет определять в процентном выражении от измеренного значения.

При показаниях по шкале Iи = 10 А, погрешность прибора не должна превышать

При показаниях по шкале Iи=2 А погрешность будет иной:

При показаниях по шкале Iи=25 А погрешность будет максимальной:

Вот почему важно, чтобы аналоговый прибор работал при измерениях в 2/3 рабочей шкалы.

Пример нахождения показания амперметра по относительной погрешности

Для того чтобы узнать погрешность для амперметра, имеющего класс точности 0.05/0.02, шкалу измерения 0…25 А. Δх определяют по измеряемому показанию на шкале 10А.

Поскольку класс точности задан как c/d, то расчет будет выполняться по формуле:

Нормирующее значение xN=xk=25 A,

Δх = δ пр×xN/100=0.105×25/100=0.026 A

Выбор амперметра по метрологическим характеристикам

Наиболее частым источником ошибки при измерении тока считается то, что амперметр имеет ненулевое входное сопротивление. Напряжение, возникающее на измерителе, приводит к снижению напряжения на тестируемом устройстве. Если уменьшение будет значительным, это приведет к значительно меньшему протеканию тока. Другими словами, измеритель не показывает ток, который фактически протекает в сети.

Для того чтобы максимально нивелировать эту погрешность, применяют два основных типа архитектуры измерения: шунтирующие амперметры и с обратной связью.

Погрешность, вызванная шунтирующим измерителем, определяемая в виде частного напряжения амперметра, деленная на выходное сопротивление.

Амперметры с обратной связью ближе к «идеальным». Он вырабатывает напряжение на пути обратной связи операционного усилителя с высоким коэффициентом усиления. Это напряжение также пропорционально измеряемому току, но не появляется на входе прибора. В результате чувствительные измерители с обратной связью, такие как электрометры и пикоамперметры, имеют нагрузку по напряжению, обычно ограниченную до 200 мкВ.

Для промышленных измерений наиболее часто применяются амперметры аналогового панельного типа. При их выборе следует учитывать такие моменты:

2/3 максимальной шкалы.

Важно! Внутреннее сопротивление — определяющая величина при выборе измерителя. Ее следует принимать в соответствии с величиной измеряемого импеданса, иначе это приведет к большим ошибкам измерения. Поскольку внутреннее сопротивление отражает энергопотребление самого измерителя, при измерении тока прибор с внутренним сопротивлением следует выбирать, как можно меньшим.

Видео по теме

Источник

Расчет погрешностей средств измерений

Погрешность результата измерений в значительной мере зави­сит от погрешности средств измерений, являющейся важнейшей составляющей, от которой зависит качество измерений.

Технические характеристики, оказывающие влияние на результаты и на по­грешности измерений, называются метрологическими характерис­тиками средств измерений. В зависимости от специфики и назначения средств измерений, нормируются различные наборы или комплекты метрологических характеристик. В соответствии со стандар­том метрологические характеристики средств измерений исполь­зуются для определения результата измерений и расчетной оценки характеристик инструментальной составляющей погрешности из­мерений, расчета метрологических характеристик каналов измерительных систем и оптимального выбора средств измерений.

Инструментальная погрешность измерения – погрешность из-за несовершенства средств измерений. Эта погрешность в свою очередь обычно подразделяется на основную погрешность средств измерения и дополнительную.

Основная погрешность средства измерений – это погрешность в условиях, принятых за нормальные, т.е. при нормальных значениях всех величин, влияющих на результат измерения (температуры, влажности, напряжения питания и др.):

Δ=а или Δ=(а+bх), (1.1)

где Δ и хвыражаются в единицах измеряемой величины.

Абсолютной погрешностью прибора называется разность между показанием прибора и действительным значением измеряемой величины:

(1.2)

Поправкой прибора называется разность между действительным значением измеряемой величины и показанием прибора. Численно поправка равна абсолютной погрешности, взятой с обратным знаком:

=-Δх. (1.3)

Дополнительная погрешность возникает при отличии значений влияющих величин от нормальных. Обычно различают отдельные составляющие дополнительной погрешности, например, температурную погрешность, погрешность из-за изменения напряжения питания и т.п.

. (1.4)

. (1.5)

где x_n — нормирующее значение.

Пределы допускаемой приведенной основной погрешности, определяемой по формуле (1.5),

, (1.6)

Для средств измерений, используемых в повседневной практике, принято деление по точности на классы.

Класс точности средств измерений — обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.

Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполненных с помощью этих средств.

Классы точности устанавливаются стандартами, содержащими технические требования к средствам измерений, подразделяемым по точности. Средства измерений должны удовлетворять требованиям, предъявляемым к метрологическим характеристикам, установленным для присвоенного им класса точности как при выпуске их из производства, так и в процессе эксплуатации.

Пределы допускаемых дополнительных погрешностей устанавливают в виде дольного значения предела допускаемой основной погрешности для всей рабочей области влияющей величины или ее интервала, отношения предела допускаемой дополнительной погрешности, соответствующей интервалу величины, к этому интервалу, либо в виде зависимости предела, допускаемой относительной погрешности от номинальной или пре­дельной функции влияния. Пределы всех основных и дополнительных допускаемых погрешностей выражаются не более чем двумя значащими цифрами, причем погрешность округления при вычислении пределов не должна превышать 5 %.

Обозначения классов точности наносятся на циферблаты, щитки и корпуса средств измерений, приводятся в нормативно-технических документах.

Пример

Десять одинаковых осветительных ламп соединены параллельно. Ток каждой лампы I_л = 0,3 А. Определить абсолютную и отно­сительную погрешности амперметра, включенного в неразвет­вленную часть цепи, если его показания I₁ = 3,3 А.

1. Ток в неразветвленной части цепи

.

2. Абсолютная погрешность

.

3. Относительная погрешность

.

Задачи

2. Было проведено однократное измерение термо-ЭДС автоматическим потенциометром класса 0,5 градуировки ХК со шкалой 200…600°С. Указатель стоит на отметке 550°С. Оцените максимальную относительную погрешность измерения термо-ЭДС потенциометром на отметке 550°С. Условия работы нормальные.

3. Определить относительную погрешность измерения напряжения 100 В вольтметром класса точности 2,5 на номинальное напряжение 250 В.

4. Амперметр с верхним пределом измерения 10А показал ток 5,3 А при его действительном значении, равном 5,23 А. Определить абсолютную, относительную и относительную приведенную погрешности амперметра, а также абсолютную поправку.

5. При поверке амперметра с пределом измерения 5А в точках шкалы: 1; 2; 3; 4 и 5А получены следующие показания образцового прибора: 0,95; 2,06; 3,05; 4,07 и 4,95 А. Определить абсолютные, относительные и относительные приведенные погрешности в каждой точке шкалы и класс точности амперметра.

6. При поверке технического амперметра получены следующие показания приборов: поверяемый амперметр 1—2—3—4—5—4—3—2—1А,

образцовый ход вверх l,2—2,2—2,9—3,8—4,8 А

амперметр ход вниз 4,8—3,9—2,9—2,3—1,1 А.

Найти абсолютную и относительную приведенную погрешности, а также вариации показаний прибора. Определить, к какому классу точности его можно отнести.

7. Поверка вольтметра методом сравнения с показаниями образцового прибора дала следующие результаты:

при увеличении при уменьшении

Определить наибольшую относительную приведенную погрешность и класс точности.

8. Определить относительную погрешность измерения напряжения, если показание вольтметра класса 1,0 с пределом измерения 300 В составило 75 В.

9. Определить абсолютную и относительную погрешности измерений, если вольтметр с пределом измерений 300 В класса 2,5 показывает 100 В.

11. В цепь током 15 А включены три амперметра со следующими параметрами: класса точности 1,0 со шкалой на 50 А, класса 1,5 на 30 A и класса 2,5 на 20 А. Определить, какой из амперметров обеспечит большую точность измерения тока в цепи.

12. Имеются три вольтметра: класса 1,0 номинальным напряжением 300 В класса 1,5 на 250 В и класса 2,5 на 150 В. Определить, какой из вольтметров обеспечит большую точность измерения напряжения 130 В.

13. Показания амперметра I₁= 20 А, его верхний предел I_н = 50 А; показания образцового прибора, включенного последовательно, I = 20,5 А. Определить относительную и приведенную от­носительную погрешности амперметра.

14. Определить относительную погрешность измерения тока 10 А амперметром с I_н = 30 А класса точности 1,5.

15. При измерении мощности ваттметром класса точности 0,5, рассчитанным на номинальную мощность Р_н = 500 Вт записано показание Р₁=150 Вт. Найти пределы, между которыми заключено действительное значение измеряемой мощности.

16. Сопротивления включены по схеме, изображенной на рис.1.1. Ток в неразветвленной части цепи I=12 А, в сопротивлениях I₁=3 А; I₂=5А. Чему равны абсолютная и относительная погрешности амперметра, указанного на схеме, если его показания I₃=3,8 А?

R₁

Рис.1.1. Схема измерения тока

Источник