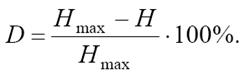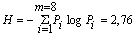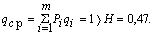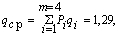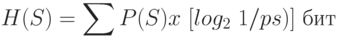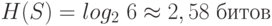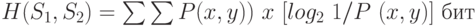Как рассчитать энтропию алфавита
Энтропия и избыточность алфавита
Энтропия алфавита – это количество информации, приходящееся на один символ. Символы равновероятного алфавита несут максимальную информационную нагрузку
Алфавиты природных языков не являются равновероятными. Например, относительная частота появления отдельных символов русского языка изменяется от 0,175 до 0,002.
Вследствие статистических свойств алфавита информационная нагрузка на один символ снижена на
Избыточностью алфавита называется уменьшение информационной нагрузки на один символ вследствие неравновероятности и взаимозависимости появления его символов.
Информационная избыточность, характеризующая относительную недогруженность алфавита рассчитывается так:
Равномерные коды
Равномерные кодыхарактеризуются минимальной разрядностью кодовых слов, которая рассчитывается по формуле
где N – объем исходного алфавита А;
M – объем кодового алфавита В;
[logM N] означает целую часть числа logM N
Рассмотрим эти формулы для случая двоичного кодирования (т. е. при М = 2). Минимальная разрядность равномерного кода для алфавита объемом 8 символов будет равна
А для 9-буквенного алфавита
Неравномерные коды
Неравномерные кодыхарактеризуются средней длиной кодового слова
li – длина кодового слова i-го символа;
pi – вероятность появления i-го символа;
N – объем исходного алфавита.
Например, если алфавит А = <a, b, c, d, e> с вероятностями появления символов в сообщении (pa = 0,5; pb = 0,2; pc = 0,1; pd = 0,15; pe = 0,05) закодирован двоичным неравномерным кодом (a – 0; b – 10; c – 1110; d – 110; e – 1111), то средняя длина кодового слова для такого алфавита будет
Таким образом, средняя длина кодового слова есть сумма длин всех кодовых слов, взятых с весом, равным вероятности появления кодируемого символа.
Количество и объем информации
Оптимальное кодирование
Метод Шеннона – Фано
Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в строку).
Шаг 2. Не меняя порядка символов, делим их на две группы так, чтобы суммарные вероятности символов в группах были по возможности равны.
Шаг 3. Приписываем группе слева «0», а группе справа «1» в качестве элементов их кодов.
Шаг 4. Просматриваем группы. Если число элементов в группе более одного, идем на Шаг 2. Если в группе один элемент, построение кода для него завершено.
Метод Хаффмана
Шаг 1. Упорядочиваем символы исходного алфавита в порядке невозрастания их вероятностей. (Записываем их в столбец).
Шаг 2. Объединяем два символа с наименьшими вероятностями. Символу с большей вероятностью приписываем «1», символу с меньшей – «0» в качестве элементов их кодов.
Шаг 3. Считаем объединение символов за один символ с вероятностью, равной сумме вероятностей объединенных символов.
Шаг 4. Возвращаемся на Шаг 2 до тех пор, пока все символы не будут объединены в один с вероятностью, равной единице.
Избыточность источника сообщений
Из энтропийных оценок источников сообщений, ясно, что она зависит от статических характеристик самих сообщений. Энтропия максимальна при равномерном появлении букв на любом месте сообщения. Для характеристики источника сообщений с различным алфавитом представляет интерес сравнение фактической энтропии источника с максимально возможной. В этом смысле введено понятие избыточности источника сообщений или избыточности алфавита.
M – количество различных букв в алфавите;
H(X) – средняя энтропия на одну букву.
Избыточность источника R показывает на сколько хорошо используются буквы в данном источнике. Чем меньше R, тем большее количество информации вырабатывается источником на одну букву. Однако, не всегда необходимо стремиться к R = 0. С повышением избыточности повышается помехоустойчивость (надежность) источника. Выяснение количества избыточности важно потому, что мы должны вводить ее разумно, чтобы получить максимальный эффект помехозащищенности, а не полагаться на стихию. Например, избыточность любого языка оказывается порядка 50-70%, то есть если бы все буквы имели одинаковую вероятность использования и можно было бы использовать любые комбинации букв, то среднюю длину слова можно было бы значительно уменьшить. Однако разбираться в этой записи было бы значительно труднее, особенно при наличии ошибок (лектора или студента).
Современные системы связи построены без учета ограничений, существующих в языке, а поэтому не достаточно эффективны, так как они приспособлены для передачи равновероятных букв алфавита, которые могут следовать друг за другом в любых комбинациях.
Колоссальная избыточность присуща телевизионным изображениям: естественно передавать не весь кадр, а только информацию соответствующую тому, чем отличается один кадр от другого. Этим можно существенно сократить требуемую (в среднем) полосу частот.
Различают две составляющие избыточности:
где H(X) – энтропия для букв, когда они неравновероятны и взаимосвязаны;
H1(X) – энтропия для букв, когда они статистически не взаимосвязаны и неравновероятны.
Но статистические связи между элементами укрупненного алфавита падают Rс ≈ 0; следовательно возрастает неравномерность употребления отдельных букв алфавита M2, то есть Rр2 >> Rр1; Rр2 ≈ R1 ≈ R2.
Доказательство, что R1 ≈ R2 сводится к следующему:
Из свойства аддитивности информации следует, что в одном элементе второго алфавита содержится столько же информации, сколько ее содержится в n элементах первичного алфавита. Среднее количество информации на один элемент первого алфавита – H1; математическое ожидание на n элементов первого алфавита – n · H1 равно информации на один элемент второго алфавита H2(X) = n · H1.
2. Избыточность второго алфавита
Избыточность языка подсчитывается по формуле:
где Hmax = log M, а M – число букв в алфавите.
а 0; 1; 2… – количество букв между которыми учитываются взаимосвязи.
Примеры
1. Во сколько раз больше содержится информации на странице текста для иностранца, начавшего изучать новый для себя язык (например, русский) и для носителя языка?
Ответ. Для носителя языка среднее количество информации на одну букву определяется как Hязыка ≈ H30 = 1.35 бит ⁄буква, а для иностранца, плохо знающего словарь и не учитывающему взаимосвязь букв между собой H = H0 или H1, что соответствует

То есть на странице текста для носителя языка содержится информации в
раза меньше информации, чем для иностранца. http://peredacha-informacii.ru/ Частичное знание словаря и закономерностей языка уменьшает эту разницу.
2. Во сколько раз удлиняется текст в деловых бумагах, если их избыточность составляет 90÷95%?
Ответ. При такой избыточности энтропия на одну букву составляет:


В то время как в письменной речи: H∞(X) = 0.87÷1.37 бит ⁄буква.
Текст удлиняется в 
Энтропия алфавита
2. Энтропия алфавита
Эту избыточность можно устранить, если перейти к кодированию достаточно большими блоками.
Так как вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако, при побуквенном кодировании мы никакого эффекта не получим. Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна
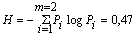
т.е. оказывается
При кодировании блоков, содержащих по две буквы, получим коды:
| Блоки | Вероятности | Кодовые комбинации | ||
| номер разбиения | ||||
| 1 | 2 | 3 | ||
| x1x1 | 0,81 | 1 | ||
| x1x2 | 0,09 | 0 | 1 | |
| x2x1 | 0,09 | 0 | 0 | 1 |
| x2x2 | 0,01 | 0 | 0 | 0 |
Так как знаки статистически не связаны, вероятности блоков определяют как произведение вероятностей составляющих знаков.
Среднее число символов на блок
а на букву 1,29/2 = 0,645, т.е. приблизилось к Н = 0,47 и таким образом удалось повысить эффективность кодирования.
Кодирование блоков, содержащих по три знака, дает еще больший эффект:
Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков не связано с учетом все более далеких статистических связей, т.к. нами рассматривались алфавиты с независимыми знаками.
Повышение эффективности определяется лишь тем, что набор вероятностей получившихся при укрупнении блоков можно делить на более близкие по суммарным вероятностям подгруппы.
От указанного недостатка свободен метод Хаффмона.
Эта методика гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Для двоичного кода метод Хаффмона сводится к следующему. Буквы алфавита сообщений выписывают в основной столбец таблицы в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятности букв, не участвующих в объединении и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются.
Процесс продолжается до тех пор, пока не получат единственную вспомогательную букву с вероятностью, равной единице.
Используя метод Хаффмона, осуществим эффективное кодирование ансамбля из восьми знаков:
| Знаки | Вероятности | Вспомогательные столбцы | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| x1 | 0,22 | 0,22 | 0,22 | 0,26 | 0,32 | 0,42 | 0,58 | 1 | 01 |
| x2 | 0,20 | 0,20 | 0,20 | 0,22 | 0,26 | 0,32 | 0,42 | 00 | |
| x3 | 0,16 | 0,16 | 0,16 | 0,20 | 0,22 | 0,26 | 111 | ||
| x4 | 0,16 | 0,16 | 0,16 | 0,16 | 0,20 | 110 | |||
| x5 | 0,10 | 0,10 | 0,10 | 0,16 | 100 | ||||
| x6 | 0,10 | 0,10 | 1011 | ||||||
| x7 | 0,04 | 0,06 | 10101 | ||||||
| x8 | 0,02 | 10100 | |||||||
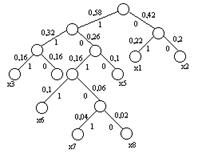
Для наглядности построим кодовое дерево. Из точки, соответствующей вероятности 1, направляем две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей 0.
Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до вероятности каждой буквы.
Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.
Совершенно секретные системы
Энтропия и неопределенность
Так как в данной формуле используется двоичный логарифм, то энтропия измеряется в битах, что общепринято в криптографии, теории информации и в компьютерных науках.
Определим энтропию второго источника:
Неопределенность оказалась равной одному биту. Найдем теперь энтропию третьего источника:
Неопределенность у третьего источника меньше, чем у второго, так как из двух возможных сообщений, генерируемых третьим источником, одно более вероятно, чем другое.
Норма языка и избыточность сообщений
Для каждого языка можно ввести величину, называемую нормой языка r и определяемую по формуле
Абсолютной нормой языка R называют максимальное количество бит информации, которое может быть передано одним символом рассматриваемого языка, при условии, что все последовательности символов равновероятны. Абсолютная норма языка, алфавит которого состоит из L символов, может быть вычислена как
Для русского языка, алфавит которого состоит из 33 букв, абсолютная норма языка
Избыточность языка D оценивают как
Минимальной избыточностью сообщений D = 0 обладал бы язык, в котором все символы равновероятны и могут встречаться в сообщениях независимо друг от друга в любом порядке.
Понятие совершенно секретной системы
Криптографическая система называется совершенно секретной, если анализ зашифрованного текста не может дать никакой информации об открытом тексте, кроме, возможно, его длины.
На практике возможна следующая реализация совершенно секретной системы, называемая одноразовая лента (или одноразовый блокнот, или шифр Вернама по имени американского инженера, предложившего эту систему в первой половине ХХ века). Будем предполагать, что процессу шифрования подвергаются двоичные данные. На передающей и приемной сторонах подготавливаются две одинаковые ленты, например, магнитные. Они содержат ключ шифрования. На передающей стороне лента помещается в устройство шифрования, а на принимающей стороне – в идентичное устройство, используемое для расшифрования. Когда отправитель хочет передать сообщение, он складывает по модулю два один бит исходного сообщения и один бит с магнитной ленты. После этого лента перемещается в следующее положение и можно шифровать второй бит сообщения, используя второй бит ключа. Таким образом шифруется все сообщение. На принимающей стороне лента с ключом используется аналогично.
Например, пусть исходное сообщение m содержит следующие двоичные цифры:
Предположим, в качестве ключевой используется последовательность:
F. Теория информации
В этом приложении мы обсуждаем несколько концепций теории информации, которые связаны с темами, рассмотренными в этой книге.
F.1. Измерение информации
Как мы можем измерить информацию в событии? Сколько информации нам доставляет событие? Давайте ответим на эти вопросы с помощью примеров.
Вообразите человека, сидящего в комнате. Глядя из окна, он может ясно видеть, что сияет солнце. Если в этот момент он получает сообщение (событие) от соседа, который говорит «Хороший день», это сообщение содержит какую-либо информацию? Конечно нет! Человек уже уверен, что это день и погода хорошая. Сообщение не уменьшает неопределенности его знаний.
Вообразите, что человек купил лотерейный билет. Если друг звонит, чтобы сказать, что он выиграл первый приз, это сообщение (событие) содержит информацию? Конечно да! Сообщение содержит много информации, потому что вероятность выигрыша первого приза является очень маленькой. Приемник сообщения потрясен.
F.2. Энтропия
Этот пример показывает, что результат бросания правильной монеты дает нам 1 бит информации (неопределенность). При каждом бросании мы не знаем, каков будет результат, поскольку две возможности одинаково вероятны.
Этот пример показывает, что результат бросания неправильной монеты дает нам только 0,8 битов информации (неопределенность). Количество информации здесь меньше, чем количество информации в Примере F.3, потому что мы ожидаем получить «орлов» большее число раз, чем «решек».
Может быть доказано, что для распределения вероятностей с n возможными результатами максимальная энтропия может быть достигнута, только если все вероятности равны (все результаты одинаково вероятны). В этом случае максимальная энтропия
Предположим, что бросается шестигранная игральная кость. Энтропия испытания равна
Можно доказать, что для распределения вероятностей с n возможными результатами, получается минимальная энтропия тогда и только тогда, когда все время получается один из результатов. В этом случае минимальная энтропия
Другими словами, эта формула определяет нижний предел энтропии для любого набора вероятностей.
Другие соотношения
Приведем здесь без доказательства некоторые другие соотношения для энтропии:
Второе и третье соотношения справедливы, если S1 и S2 статистически независимы.
Пример F.8
Совершенная секретность
Это означает, что H (P | C) = H (P)
Шеннон показал, что в криптографической системе, если (1) ключи возникают с равной вероятностью и (2) для каждого исходного текста и каждого зашифрованного текста есть уникальный ключ, то криптографическая система обеспечивает совершенную секретность. Доказательство использует тот факт, что в этом случае распределения вероятностей ключей, исходного текста и зашифрованного текста имеют один и тот же размер.
F.3. Энтропия языка
Интересно связать концепцию энтропии с естественными языками, такими как английский язык. В этом разделе мы касаемся некоторых пунктов, связанных с энтропией языка.
Энтропия произвольного языка
Энтропия английского языка
Избыточность
Шифр подстановки использует множество ключей, состоящих из 26 ключей, и алфавит из 26 символов. Используя избыточность 0,70 для английского языка, определяем интервал однозначности:
Это означает, что зашифрованный текст должен содержать по крайней мере 27 символов, для того чтобы Ева могла уникально найти исходный текст.
Шифр сдвига использует множество из 26 ключей и алфавит из 26 символов. Используя избыточность 0,70 для английского языка, интервал однозначности определяем следующим соотношением:
Это означает, что Еве необходимо иметь по крайней мере 2 символа зашифрованного текста, чтобы уникально найти исходный текст. Конечно, это весьма приблизительная оценка. В фактической ситуации Ева нуждается в большем количестве символов, чтобы нарушить код.