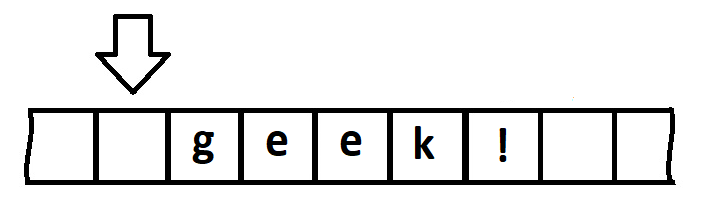Как пользоваться машиной тьюринга программой
Машина Тьюринга: описание и примеры машин Тьюринга
Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.
Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
Функции машины Тьюринга
В решении алгоритмов часто требуется реализация функции. В зависимости от возможности написания цепочки для вычисления, функцию называют алгоритмически разрешимой или неразрешимой. В качестве множества натуральных или рациональных чисел, слов в конечном алфавите N для машины рассматривается последовательность множества В – слова в рамках двоичного кодового алфавита В=<0.1>. Также в результат вычисления учитывается «неопределенное» значение, которое возникает при «зависании» алгоритма. Для реализации функции важно наличие формального языка в конечном алфавите и решаемость задачи распознавания корректных описаний.
Программа для устройства
Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 0 | 1 | 2 | 3 | . | 7 | 8 | 9 | |
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
тренажер для изучения универсального исполнителя
Что это такое?
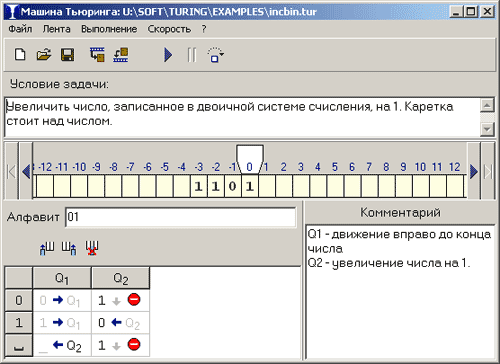
Тренажёр «Машина Тьюринга» — это учебная модель универсального исполнителя (абстрактной вычислительной машины), предложенного в 1936 году А. Тьюрингом для уточнения понятия алгоритма. Согласно тезису Тьюринга, любой алгоритм может быть записан в виде программы для машины Тьюринга. Доказано, что машина Тьюринга по своим возможностям эквивалентна машине Поста и нормальным алгорифмам Маркова.
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q=
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей:
Использование и скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.
Скачать
Пароль к архиву — kpolyakov.spb.ru
В архив включены следующие файлы:
| turing.exe | основная программа — учебная модель «Машины Тьюринга» |
| EXAMPLES | подкаталог с примерами программ для тренажера «Машина Тьюринга« |
После распаковки архива программа находится в работоспособном состоянии и не требует никаких дополнительных установок.
Наследие Тьюринга: машина, тест и полнота
Что такое машина Тьюринга
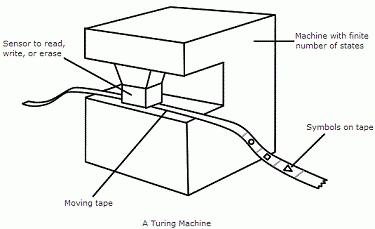
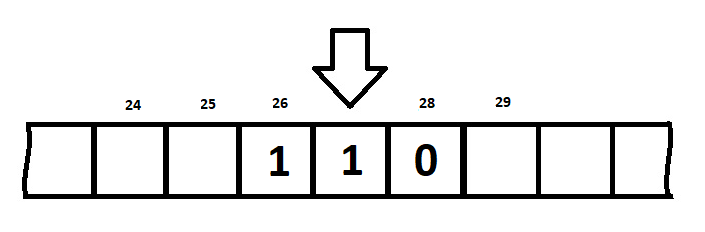
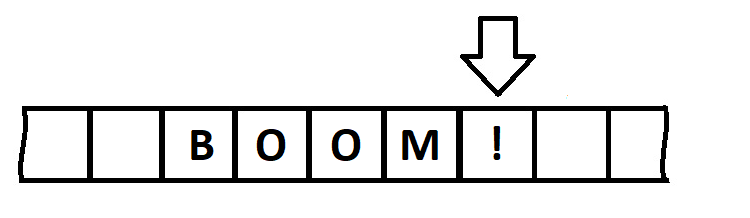
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
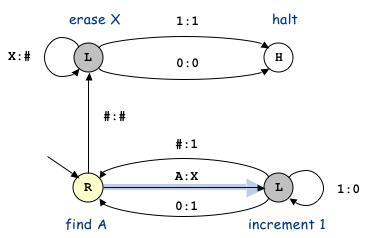
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Если вы не учились профессии программиста в вузе или не ходили в специальную школу, то, возможно «Машина Тьюринга» для вас просто дешифратор из курса истории или фильма «Игра в имитацию». В действительности всё немного сложнее, любому уважающему себя программисту необходимо знать и понимать, что это такое.
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Реализация алгоритма в машине Тьюринга
На ряде примеров покажем, как строятся тьюринго-вы машины, реализующие некоторые простые арифметические алгоритмы.
Пример 1.Реализация в машине Тьюринга алгоритма перехода от n к n+1 в десятичной системе счисления.
Пусть дана десятичная запись натурального числа п и требуется указать десятичную запись числаn+1, т.е. вычислить функциюf(n) = п + 1.
Ясно, что здесь внешний алфавит машины должен содержать все цифры О, 1, 2, 3, 4, 5, 6, 7, 8, 9 исимвол пустой клеткиaQ. Числоп будем записывать в десятичной системе на ленте, причем цифры будут помещаться по одной в каждой клетке подряд без пропусков.
Чтобы решить поставленную задачу, машина должна в первом такте работы стереть последнюю цифру числа л, заменить ее цифрой на единицу большей и перейти в стоп-состояние, если последняя цифра была меньше цифры 9.
Бели же последняя цифра числа n была 9, то машина должна, стерев цифру 9, записать в освободившуюся клетку цифру 0 и произвести сдвиг влево к соседнему более высокому разряду, оставаясь в том же начальном состоянии. Здесь во втором такте работы машина должна прибавить единицу к цифре более высокого разряда.
Очевидно, что в случае сдвига влево, управлявшая головка машины может выйти на пустую клетку в случае, когда цифры более высокого разряда нет. При этом машина вписывает в пустую клетку цифру 1.
Из сказанного следует, что при реализации алгоритма вычисления функцииf(n) = n + 1машина может пребывать лишь в двух состоянияхql иq0.
Таким образом, машина Тьюринга, реализующая алгоритм перехода от n кn+1 в десятичной системе счисления будет иметь вид:
| a0 | |||||||||||
| q1 | 1 q0 | 1 q0 | 2 q0 | 3 q0 | 4 q0 | 5 q0 | 6 q0 | 7 q0 | 8 q0 | 9 q0 | 0 q1 |
На рис. 4 и 5 выписаны соответствующие конфигурации для n = 183 и n = 399:
| a0 399 a0 q1 | |
| a0 183 a0 q0 | a0 390 a0 q1 |
| a0 184 a0 q1 | a0 300 a0 q1 |
| a0 400 a0 q0 |
Пример 2. Алгоритм сложения натуральных чисел» Пусть на ленту подается два числа, заданных наборами палочек; например, 2 и 3. Нужно сложить эти числа.
Будем обозначать символ сложения звездочкой. Таким образом, на ленте машины будет записано слово
А0 (1) Требуется предложить функциональную схему, которая, будучи примененной, к слову (1), давала бы в результате сумму чисел 2 и 3, то есть слово а0
А0 (2) Опишем процесс работы машины для решения задачи. Пусть в начальный момент обозревается самая левая палочка. Ее нужно сдвинуть вправо, минуя все палочки и звездочку до тех пор, пока не будет достигнута первая пустая клетка. В эту пустую клетку вписывается первая палочка. Затем нужно вернуться за второй палочкой и ее перенести вправо так же, как это делалось с первой палочкой. После этой процедуры нужно вернуться к звездочке, стереть ее и остановиться. Изобразим все такты работы машины в виде соответствующих конфигураций: 1. a0 ||*
Машина тьюринга сложение двух чисел
»Я не знаю, кто я — Тьюринг, которому снится, что он машина,
или машина, которой снится, что она Тьюринг!».
Дао Программирования
Для более близкого знакомства с машиной Тьюринга, рекомендую её имитатор Algo2000 Зартидова Радика. На мой взгляд — это лучшая реализация имитатора машины Тьюринга.
Машина тьюринга сложение двух чисел
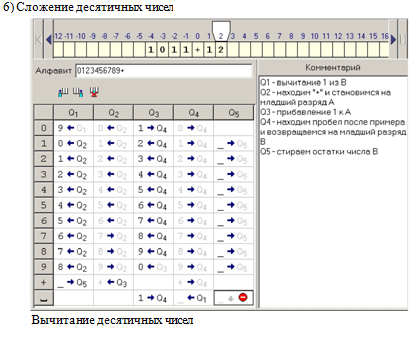
6.
Составьте программы для машины Тьюринга, которые выполняют
сложение и вычитание двух чисел в десятичной системе счисления.
ответ
Если при стирании ведущего нуля автомат «попадает» на минус — можно остановить. На ленте останется результат вычетания большего числа из меньшего (отрицательный результат).
Т.е. в ячейке в ряду «-» и колонке «О5» изменить команду: оставить «-«, остаться на месте, останов.
Условие — машина Тьюринга
Число представлено в двоичном формате в различных конечных автоматах, например, 5 представлено как (101), но в случае добавления с использованием машины Тьюринга используется унарный формат. В унарном формате число представлено либо всеми единицами, либо всеми нулями. Например, 5 будет представлен последовательностью из пяти нулей или пяти единиц. 5 = 1 1 1 1 1 или 0 0 0 0 0. Позволяет использовать нули для представления.
Для добавления 2 чисел с использованием машины Тьюринга оба эти числа приводятся в качестве входных данных для машины Тьюринга, разделенных «с».
Примеры — (2 + 3) будут заданы как 0 0 c 0 0 0:
Подход используется —
Преобразуйте 0 в первом числе в X, а затем пройдитесь по всему вводу и преобразуйте первый пробел в 0. Затем двигайтесь влево, игнорируя все 0 и «c». Пройдите позицию рядом с X, а затем повторяйте ту же процедуру до тех пор, пока мы не получим «c» вместо X при возврате. Преобразовать c в пустую и сложение завершено.
Шаг 1: конвертируйте 0 в X и переходите к шагу 2. Если символ «с», то конвертируйте его в пробел (B), двигайтесь вправо и переходите к шагу 6.
Шаг 2: Продолжайте игнорировать 0 и двигайтесь вправо. Не обращайте внимания на «c», двигайтесь вправо и переходите к шагу 3.
Шаг 3: продолжайте игнорировать 0 и двигайтесь вправо. Преобразуйте пробел (B) в 0, переместитесь влево и перейдите к шагу 4.
Шаг 4: продолжайте игнорировать 0 и двигайтесь влево. Не обращайте внимания на «c», двигайтесь влево и переходите к шагу 3.
Шаг 5: продолжайте игнорировать 0 и двигайтесь влево. Не обращайте внимания на X, двигайтесь влево и переходите к шагу 1.
Главная > Документ
| Информация о документе |
| Дата добавления: |
| Размер: |
| Доступные форматы для скачивания: |
Машина Тьюринга – математическая модель процессов преобразования информации, с ее помощью можно реализовать любой алгоритм.
Эту модель можно представить как устройство, состоящее из следующих частей:
бесконечной или полу бесконечной ленты, разделенной на ячейки,
читающе — записывающей головки,
управляющего устройства, которое за один такт работы машины а) считывает из ячейки символ, б) записывает в него новый (может быть тот же) символ, в) перемещается влево, вправо или остается на месте, г) изменяет состояние.
При составлении алгоритмов на машине Тьюринга обычно используют следующие приемы: 1) машина запоминает тот или иной символ, переходя в различные состояния, 2) отметка просмотренного символа делается с помощью символов внешнего (дополнительного) алфавита.
Будем считать, что рассматриваемые выражения и строки отделяются на ленте слева и справа пробелами и лента бесконечная в оба конца.
Алгоритмы удобно записывать в виде таблицы, где заголовками столбцов являются символы допустимого алфавита, а заголовками строк – состояния машины. В ячейках стоят конфигурации машины, соответствующие определенным символам и состояниям.
Машина Тьюринга: описание и примеры машин Тьюринга
Машина Тьюринга — одно из самых интригующих и захватывающих интеллектуальных открытий 20-го века. Это простая и полезная абстрактная модель вычислений (компьютерных и цифровых), которая является достаточно общей для воплощения любой компьютерной задачи. Благодаря простому описанию и проведению математического анализа она образует фундамент теоретической информатики. Это исследование привело к более глубокому познанию цифровых компьютеров и исчислений, включая понимание того, что существуют некоторые вычислительные проблемы, не решаемые на общих пользовательских ЭВМ.
Что это и кто создал
Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье «О вычислимых числах с приложением к проблеме разрешимости», которая появилась в Трудах Лондонского математического общества.
Машина Тьюринга является вычислительным устройством, состоящим из головки чтения/записи (или «сканера») с бумажной лентой, проходящей через него. Лента разделена на квадраты, каждый из которых несет одиночный символ — «0» или «1». Назначение механизма состоит в том, что он выступает и как средство для входа и выхода, и как рабочая память для хранения результатов промежуточных этапов вычислений.
Из чего состоит устройство
Каждая такая машина состоит из двух составляющих:
Как работает механизм
Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.
Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.
Свойства механизма
Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:
Функции машины Тьюринга
Программа для устройства
Программы для механизма Тьюринга оформляются таблицами, в которых первые строка и столбец содержат символы внешнего алфавита и значения возможных внутренних состояний автомата — внутренний алфавит. Табличные данные являются командами, которые воспринимает машина Тьюринга. Решение задач происходит таким образом: буква, считываемая головкой в ячейке, над которой она в данный момент находится, и внутреннее состояние головки автомата обусловливают, какую из команд необходимо выполнять. Конкретно такая команда находится на пересечении символов внешнего алфавита и внутреннего, находящихся в таблице.
Составляющие для вычислений
Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.
Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.
Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.
Алгоритм для автомата
Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:
Таким образом, при написании программ для каждой пары символов либо положений необходимо точно описать три параметра: ai – элемент из выбранного алфавита A, направление сдвига каретки («←” влево, «→” вправо, «точка” — отсутствие перемещения) и qk — новое состояние устройства. К примеру, команда 1 «←” q2 имеет значение «заместить символ на 1, сдвинуть головку каретки влево на один шаг-ячейку и сделать переход в состояние q2”.
Машина Тьюринга: примеры
Пример 1. Дана задача построить алгоритм, прибавляющий единицу к последней цифре заданного числа, расположенного на ленте. Входные данные – слово – цифры целого десятичного числа, записанные в последовательные ячейки на ленту. В первоначальный момент устройство располагается напротив самого правого символа – цифры числа.
Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:
| a0 | 0 | 1 | 2 | 3 | . | 7 | 8 | 9 | |
| q1 | 1 H q0 | 1 H q0 | 2 H q0 | 3 H q0 | 4 H q0 | . | 8 H q0 | 9 H q0 | 0 λ q1 |
Здесь q1 — состояние изменения цифры, q0 — остановка. Если в q1 автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q0, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q1. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q0 – остановка.
| a0 | ( | ) | |
| q1 | a0 H q0 | ( П q2 | ) П q1 |
| q2 | a0 H q0 | ( П q2 | ) λ q3 |
| q3 | a0 H q0 | a0 П q3 | a0 П q1 |
Состояние q1: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q2; если определен “a0”, то остановка.
Состояние q2: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q3.
Состояние q3: осуществить удаление сначала символа “(”, а затем “)” и перейти в q1.
Элементарная Машина Тьюринга
Введение
Машина Тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.[1]
Описание формальной модели алгоритма на основе рекурсивных функций
Определение понятия примитивно рекурсивной функции является индуктивным. Оно состоит из указания класса базовых примитивно рекурсивных функций и двух операторов (подстановки и примитивной рекурсии), позволяющих строить новые примитивно рекурсивные функции на основе уже имеющихся.
К базовым примитивно рекурсивным фунциям относят:
Задание: доказать примитивную рекурсивность функции «ближайшее к n простое число».
Протестируем приведённую выше схему вычисления ближайшего к 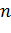
В качестве параметра возьмём простое число 5.
Рисунок 1.1 — Тест алгоритма на числе 5
В качестве параметра возьмём 15:
Рисунок 1.2 — Тест алгоритма на числе 15
Аналитическая модель Машины Тьюринга
Элементарная Машина Тьюринга
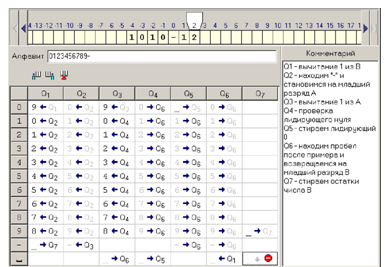
Задание: реализовать Машину Тьюринга для вычисления функции получения остатка от деления двух чисел в унарном коде с сохранением данных. Описать полученную машину тремя способами: правилами переходов, таблицей состояний и графом состояний.
Во входных данных находятся делимое и делитель в унарном коде, разделённые символом «*». В выходных данных к входным должна добавиться конструкция «= », где — результат вычислений в унарном коде.
Пример входных данных: 11111111*111
Пример выходных данных: 11111111*111=11
Ниже приведено описание элементарной машины Тьюринга тремя способами: списком правил переходов, таблицей состояний и графом:
| > Рисунок 2.1 — Правила переходов для Машины Тьюринга |
2.1.6 Описание Машины Тьюринга таблицей состояний
Таблица 2.1 — Таблица состояний Машины Тьюринга
| qa | * | λ | _ | = | # |
| q0 | |||||
| q1 |
Продолжение таблицы 2.1
| qa | * | λ | _ | = | # |
| q2 | |||||
| q3 | |||||
| q4 | |||||
| q5 | |||||
| q6 | |||||
| q7 | |||||
| q8 | |||||
| q9 | |||||
| q10 | |||||
| q11 |
Рисунок с графом переходов.
Рисунок 2.2 — Граф переходов
На рисунке 2.3 приведено тестирование работы Машины Тьюринга для входных данных 11111*11.
| Трассировка алгоритма на каком-то контрольном значении Рисунок 2.3 — Тестирование Машины Тьюринга |
2.2 Композиция Машин Тьюринга
Построить композицию Машин Тьюринга для вычисления ближайшего к s простого числа в унарном коде без сохранения исходных данных.
Пример входных данных: 111111
Пример выходных данных: 11111
Ниже привдена блок-схема алгоритма, реализующего вычисление заданного алгоритма:
Рисунок 2.4 — Блок схема алгоритма поиска ближайшего к s простого числа
В композиции будут участвовать следующие Машины Тьюринга:
— 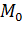
— 
— 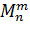
— 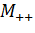
| СХЕМА КОМПОЗИЦИИ ИЗ 3 ЛАБЫ Рисунок 2.5 — Композиция Машин Тьюринга |

Теперь распишем машину 
В композиции будут участвовать машины:
— 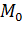
— 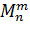
— 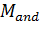
— 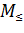
— 
— 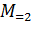
— 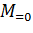
— 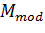
— 
— 
— 
СХЕМА КОМПОЗИЦИИ ИЗ 3 ЛАБЫ
Рисунок 2.6 — Композиция машины проверки на простоту