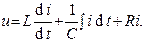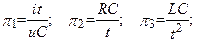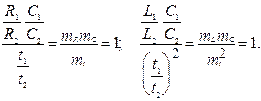говорят что имеет место явление автомодельности если
Большая Энциклопедия Нефти и Газа
Явление автомодельности дает возможность упрощения дифференциальных уравнений и условий однозначности. Члены уравнений ( или условий однозначности), учитывающие факторы, относительно которых процесс оказывается автомодельным, могут быть опущены или видоизменены. [1]
Явлением автомодельности называется независимость характера движения жидкости от критерия Рейнольдса. Поэтому при высоких скоростях потока, когда наступает автомодельность процесса, условие подобия Re idem можно не соблюдать. [2]
В общем случае ( когда отсутствует явление автомодельности ) при движении жидкости по трубам коэффициенты гидравлического трения, коэффициенты сопротивления обтекаемых тел, коэффициенты расхода при истечении из отверстий и насадок и другие зависят от числа Рейнольдса. Однако, если числа Рейнольдса больше некоторых предельных значений ( Reap), все эти коэффициенты, обычно входящие в рабочие уравнения существующих расходомеров, приобретают постоянные и независящие от числа Рейнольдса значения. [3]
В общем случае ( когда отсутствует явление автомодельности ) при движении жидкости по трубам коэффициенты гидравлического трения, коэффициенты сопротивления обтекаемых тел, коэффициенты расхода при истечении из отверстий и насадок и другие зависят от числа Рейнольдса. Однако, если числа Рейнольдса становятся больше некоторых предельных значений ( Re p), все эти коэффициенты, обычно входящие в рабочие уравнения существующих расходомеров, приобретают постоянные и независящие от числа Рейнольдса значения. [4]
В общем случае ( когда отсутствует явление автомодельности ) при движении жидкости по трубам коэффициенты гидравлического трения, коэффициенты сопротивления обтекаемых тел, коэффициенты расхода при истечении из отверстий и насадок и другие зависят от числа Рейнольдса. Однако, если числа Рейнольдса больше некоторых предельных значений ( Reap), все эти коэффициенты, обычно входящие в рабочие уравнения существующих расходомеров, приобретают постоянные и независящие от числа Рейнольдса значения. [5]
В некоторых случаях: осуществить полное подобие в натурном образце и модели практически невозможно. Тогда применяется приближенное моделирование, основанное на автомодельности процесса. Сущность явления автомодельности состоит в том, что изменение какого-либо критерия в определенных пределах не оказывает влияния на протекание процесса; поэтому наобходимость соблюдения равенства этого критерия для модели и образца не требуется. [8]
ТЕПЛОМАССООБМЕН
Контрольные вопросы
9. Каковы условия подобия тепловых процессов в мо дели и образце?
Моделированием называют метод экспериментального исследования, в котором изучение какого-либо физического явления производит ся на уменьшенной модели. Идея о моделировании вытекает из того, что всякое явление, описанное в безразмерных переменных, отражает признаки группы подобных явлений.
Для того чтобы модель стала подобна образцу, необходимо выпол нить следующие условия. Моделировать можно процессы, имеющие одинаковую физическую природу и описываемые одинаковыми дифференциальными уравнениями. Условия однозначности должны быть одинаковы во всем, кроме численных значений постоянных, содержа щихся в этих условиях. Условия однозначности тре буют: геометрического подобия образца и модели, подобия условий движения жидкости во входных сечениях образца и модели, подобия физических параметров в сходственных точках образца и модели подобия температурных полей на границах жидкой среды. Кроме того, одноименные определяющие числа подобия в сходственных сечениях образца и модели должны быть численно одинаковы.
Перечисленные условия подобия для образца и модели являются необходимыми и достаточными. Однако практически точное осущест вление всех условий моделирования выполнить затруднительно. Поэтому была разработана методика приближенного моделирования, заключающаяся в стабильности и автомодельности потока и приме няющая метод локальности.
Геометрическое подобие образца и модели осуществить нетрудно. Подобное распределение скоростей во входном сечении также может быть выполнено относительно просто. Подобие физических параметров в потдке жидкости для модели и образца выполняется лишь приближенно, а подобие температурных полей у поверхностей нагрева в модели и образце осуществить очень трудно. В связи с этим применяют приближенный метод локального моделирования.
Локальное моделирование заключается в том, что подобие температурных полей осуществляется не во всем объеме аппарата, а в отдельных ее местах — сечениях, где производится исследование теплоотдачи. Равенство определяющих критериев в образце и модели может быть выполнено приближенно.
Стабильностью называют свойство вязкости жидкости всегда принимать на некотором расстоянии от входа одно и то же распределение скоростей по сечению вне зависимости от картины скоростей во входном сечении.
Явление автомодельности заключается в том, что при движении жидкости для довольно широкого диапазона скоростей имеет место почти не меняющееся распределение скорости в данном сечении, т. е. оно практически перестает зависеть от Re.
Содержание
Обзор
Самоподобный трафик Ethernet демонстрирует зависимости в большом диапазоне временных масштабов. Это должно быть контрастировано с телефонным трафиком, который является пуассоновским в процессе прибытия и отправления.
В традиционном пуассоновском трафике краткосрочные колебания усредняются, и график, охватывающий большой промежуток времени, приближается к постоянному значению.
Самоподобие в сетях с пакетной передачей данных может быть вызвано распределением размеров файлов, человеческим взаимодействием и / или динамикой Ethernet. Самоподобные и зависимые на большие расстояния характеристики в компьютерных сетях представляют собой принципиально другой набор проблем для людей, занимающихся анализом и / или проектированием сетей, и многие из предыдущих предположений, на которых были построены системы, больше не действительны при наличии самоподобие.
Распределение Пуассона
Предполагая, что прибытие по чистой случайности или прерывание по чистой случайности приводит к следующему:
Распределение с тяжелым хвостом
Говорят, что распределение имеет тяжелый хвост, если
Моделирование автомодельного трафика
Поскольку (в отличие от традиционного телефонного трафика) пакетный трафик демонстрирует самоподобные или фрактальные характеристики, традиционные модели трафика не применимы к сетям, которые несут самоподобный трафик.
С конвергенцией голоса и данных будущая мультисервисная сеть будет основана на пакетном трафике, и модели, которые точно отражают природу самоподобного трафика, потребуются для разработки, проектирования и измерения будущих мультисервисных сетей.
Предыдущая аналитическая работа, проведенная в Интернет-исследованиях, основывалась на предположениях, таких как экспоненциально распределенное взаимное прибытие пакетов, и выводы, сделанные на основе таких предположений, могут вводить в заблуждение или неверны при наличии распределений с тяжелыми хвостами.
Автомодельные случайные процессы, моделируемые распределениями Твиди
Леланд и др. Предложили математический аппарат для описания автомодельных случайных процессов. Для последовательности чисел
μ ^ знак равно E ( Y я ) <\ displaystyle <\ hat <\ mu>> = <\ text 
σ ^ 2 знак равно E ( y я 2 ) <\ displaystyle <\ hat <\ sigma>> ^ <2>= <\ text 
и автокорреляционная функция
Дисперсия, определенная из этой последовательности, будет масштабироваться по мере изменения размера ячейки, так что
тогда и только тогда, когда автокорреляция имеет предельный вид
Также можно построить набор соответствующих аддитивных последовательностей
на основе расширяющихся бункеров,
Если автокорреляционная функция демонстрирует такое же поведение, аддитивные последовательности будут подчиняться соотношению
Эти распределения Твиди характеризуются внутренней масштабной инвариантностью, и, таким образом, для любой случайной величины Y, которая подчиняется распределению Твиди, дисперсия var ( Y ) относится к среднему E ( Y ) по степенному закону,
Аддитивная форма составной модели Пуассона-гамма Твиди имеет кумулянтную производящую функцию (CGF),
Первая и вторая производные CGF при s = 0 дают среднее значение и дисперсию соответственно. Таким образом, можно подтвердить, что для аддитивных моделей дисперсия относится к среднему по степенному закону,
Производительность сети
Производительность сети постепенно снижается с увеличением самоподобия. Чем больше самоподобный трафик, тем больше размер очереди. Распределение длин очереди автомодельного трафика затухает медленнее, чем с пуассоновскими источниками. Однако дальнодействующая зависимость ничего не говорит о ее краткосрочных корреляциях, которые влияют на производительность в небольших буферах. Кроме того, агрегирование потоков самоподобного трафика обычно усиливает самоподобие («прерывистость»), а не сглаживает их, усугубляя проблему.
Самоподобный трафик демонстрирует стойкость кластеризации, которая отрицательно сказывается на производительности сети.
Многие аспекты качества обслуживания сети зависят от того, как справляться с пиками трафика, которые могут вызвать сбои сети, например:
Понятие об автомодельности.
Мы же ограничимся лишь кратким рассмотрением содержания этого понятия без уяснения которого невозможна грамотная постановка эксперимента.
Для простоты будем считать, что в интересующем исследователя процессе определяющими является силы вязкого трения т.е. зависимость (13.8) имеет вид 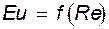


 ) происходит «вырождение», т.е. число Эйлера перестает зависеть от Re.
) происходит «вырождение», т.е. число Эйлера перестает зависеть от Re. , что далеко не всегда возможно, то в автомодельной области достаточно, чтобы
, что далеко не всегда возможно, то в автомодельной области достаточно, чтобы  было больше
было больше  . Нужно лишь помнить, что какого-то универсального значения
. Нужно лишь помнить, что какого-то универсального значения 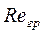 не существует, оно всегда зависит от природы изучаемого объекта, в частности, от его формы. Поэтому, как правило, задачей первого этапа экспериментального исследования является нахождение граничного значения определяющего числа подобия.
не существует, оно всегда зависит от природы изучаемого объекта, в частности, от его формы. Поэтому, как правило, задачей первого этапа экспериментального исследования является нахождение граничного значения определяющего числа подобия.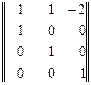
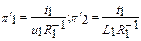
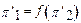 .
. .
.