дункеровские задачи что это
GuruTest
Тест на креативность от Карла Дункера
Оценить способность нестандартно мыслить можно с помощью простого психологического текста. Множество их можно найти в сети, однако самым известным остается непревзойденный тест Карла Дункера.
Карл Дункер — выдающийся немецкий психолог, который изучал мышление. Он посвятил всю жизнь исследованию работы мозга. В данной статье мы расскажем о его простом, но непревзойденном тесте на сообразительность и креативность.
Описание задачи
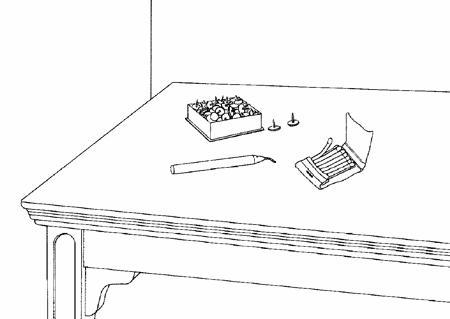
Карл Дункер создал свой знаменитый тест в 1945 году. Его начальные условия невероятно просты: у вас имеется свеча, коробок спичек и коробочка с канцелярскими кнопками. Для наглядности предлагаем вам посмотреть на иллюстрацию:
Задача заключается в том, чтобы прикрепить свечу к стене таким образом, чтобы в зажженном состоянии воск не капал на стол.
Ваша сообразительность оценивается лишь по скорости получения правильного решения. Оно не сложное, так что рано или поздно вы все равно найдете его. Не заглядывайте в конец статьи, подумайте, как бы вы решили поставленную проблему.
Решение теста на креативность
У нас есть иллюстрация, на которой нарисованы начальные условия, однако уже в этой иллюстрации есть небольшая зацепка и одновременно сложность, которая не дает нашему мозгу быстро принять решение. Дело в том, что канцелярские кнопки находятся в коробке, равно как и спички, но никто не запрещает их оттуда вытаскивать.
У вас должно получиться нечто похожее на это:
Коробок от спичек тут не играет почти никакой роли. Сначала вы оставляете пустой коробку от кнопок и ставите туда свечу, подплавив основание, чтобы она не упала. После этого прикалываете кнопками коробку к стене. Это чистая абстракция, поскольку должно быть обговорено много моментов вроде покрытия стены и прочности коробки от кнопок. Несмотря на это, ответ все же только один.
Обычно добровольцы, проходящие этот тест, начинают гадать и предлагать приколоть свечу к стене при помощи кнопок, а пустую коробку поставить на стол, чтобы в нее капал воск. Однако прикрепить свечу к стене куда проблематичнее, нежели коробку.
Чем быстрее вы дали ответ, тем более вы сообразительны и креативны. Суть теста в том, что вещи используются в непривычной для нас роли. Напоминаем, что почти все люди при проведении теста рано или поздно давали верный ответ. Это доказывает, что у всех у нас есть творческое начало.
Мы все уникальны. Каждый из нас умен по-своему, однако сообразительность и креативность можно развивать, решая логические задачи. Больше читайте и больше думайте, чтобы находить решения даже в самых странных ситуациях.
На нашем канале в Яндекс.Дзен всегда самые интересные статьи по этой теме. Обязательно подпишитесь!
Дункер
Дункер (нем. Karl Duncker, 2 февраля 1903 года, Лейпциг — 23 февраля 1940, США) — немецкий психолог, видный представитель гештальтпсихологии, один из самых выдающихся исследователей мышления.
Дункера известный прежде всего своими исследованиями в области продуктивного мышления и решения задач. Проведя многочисленные эксперименты, Дункера ввел понятие функционального значения решения задачи; открыл феномен функциональной закрепленности, заключающийся в том, что предмет использован определенным образом потом сложно использовать по-другому.
Биография
С 1930 года работал в психологическом университете в Берлине. В 1935 году покинул Германию и работал сначала в Кембридже в Ф. Ч. Бартлетта, а впоследствии в США.
Научные взгляды
Мышление и инсайт
Согласно определению Дункера, «мышление — это процесс, который с помощью инсайта (понимание) проблемной ситуации приводит к адекватным ответным действиям». Процесс, ведущий от стимула к ответному, называется инсайтного, если он непосредственно определяет содержание этого действия (в отличие от обычного высвобождения стимулом уже готовой реакции). Это необходимо, когда такое действие не выходит непосредственно из прошлого опыта.
Любую проблемную ситуацию можно рассмотреть с разных точек зрения (как совокупность элементов или как единое целое, в одной или другой структуре и т.д.). Именно этим и объясняется возможность инсайта. Психологическая структура ситуации изменяется в ходе решения задачи. Например, меняются фигурно-фоновые отношение: «части и моменты ситуации, которые раньше или совсем не осознавались, или осознавались на фоне, не тематический, вдруг выделяются, становятся главными, темой,» фигурой «, и наоборот». Могут меняться и осознаваемые (используемые) свойства (функции) элементов ситуации. Меняются отношения «часть-целое»: элементы ситуации, которые сначала воспринимались как части разных целых, начинают восприниматься как одно целое. Входя в новую структуру, элемент получает новые свойства. При этом он не перестает быть элементом первой структуры; меняется лишь точка зрения, то есть мы обращаем внимание на те его свойства, которые он имеет в другом структуре, и прекращаем интересоваться его свойствами как элемента первой структуры. «Очень возможно, что глубокие различия между людьми в том, что называют» способностью к мышлению «,» умственным одаренность «, имеют за основу большую или меньшую легкость таких переструктурувань».
Процесс решения задач
Стадии решения задачи
Согласно Дункера, процесс решения задачи выполняется следующим образом.
Функциональное значение решения не является абстрактным, то есть общим для разных конкретных задач; «Оно полностью возникает из данной проблемной ситуации», — пишет Дункера. Это доказывается тем, что при решении двух задач, имеющих общее функциональное значение решения, решение первой не помогает испытуемым в решении следующей задачи, даже если они решают их подряд.
Процесс решения является развитием проблемы. Функциональное значение решения является определенным преобразованием заданной проблемы. И каждая новая свойство будущего решения, который в процессе решения задачи принимает функциональное значение, превращает функциональное значение в новую, точнее и более определенно поставленную проблему. С каждым последующим преобразованием задачи процесс решения учитывает все больше особенностей конкретной ситуации, постепенно внедряясь в ее специфические условия и возможности. Дункера формулирует это так: «Конечная форма определенного решения в типичном случае достигается путем, ведущим через промежуточные фазы, каждая из которых имеет в отношении предыдущих фаз характер решения, а в отношении последующих — характер проблемы».
Анализ ситуации и цели
На каждой фазе решения может быть поставлен вопрос о причинах конфликта («Почему я не могу достать до банана руками?»), Что позволяет глубже понять природу конфликта и приблизиться к решению («Потому что руки слишком короткие»). Дункера называет это «анализом конфликта».
Параллельно с этим «углублением» может происходить и «горизонтальное» перемещение между несколькими функциональными значениями, причем, возвращаясь к одному из функциональных значений, человек корректирует неудачный вариант решения, на котором остановилась накануне, — по словам Дункера, ищет «в рамках предыдущей постановки вопроса другую зацепку для решения «или уточняет саму постановку вопроса.
Бывает, не функциональное значение предшествует его конкретном воплощению, а наоборот, какой-то случайно замечен элемент ситуации (например палка, замеченная обезьяной) наводит на мысль о его функциональное значение. Это может быть также результатом сознательного анализа «материала ситуации» (что я могу использовать?). Такой анализ ситуации особенно часто происходит при решении математических задач на доказательство.
Кроме описанного анализа ситуации (то есть анализа конфликта или материала) может происходить и анализ цели. Он выражается вопросами типа «Что, собственно, я хочу?», «Без чего я могу обойтись?» И т. П. («Хочу ли я, чтобы оказался там, где я, или, возможно, я — там, где банан? »). Может происходить обобщение цели («Что вообще делают, когда хотят получить что-то на расстоянии?»). Анализ цели часто применяется в решении математических задач на доказательство, когда превращается то, что надо доказать.
Задачи Дункера
Дункера пользовался в своих экспериментах математическими и практическими задачами, предлагая испытуемым рассуждать вслух во время их решения.
Математические задачи
Дункера обнаружил, что математические задачи решаются в основном с помощью анализа цели и анализа ситуации. Например: нужно выяснить, почему все числа вида «abcabc» (651 651, 274 274 и т.д.) делятся на 13. Вот несколько фрагментов из протоколов эксперимента:
(1) Возможно, каждая тройка цифр делится на 13? (2) Возможно, здесь есть какое-то правило сложения цифр, как для случая с делением на 9? (3) Это должно исходить из какого скрытого общего принципа построения — первая тройка цифр в 10 раз больше второй, 591591 есть 591 умноженное на 11, нет: умноженное на 101 (экспериментатор: «Правильно?»), Ни, 1001. или не делится 1001 на 13?
Рассуждения (3), которое привело к решению, начинается с анализа цели: утверждение, что все числа вида «abcabc» делятся на 13 превращается в утверждение, что дилимисть на 13 выходит из общих свойств чисел вида «abcabc». Затем начинается процесс анализа ситуации, направленный на поиск общих свойств чисел «abcabc», имеющие отношение к делимости. Это обычный способ решения математических (в том числе геометрических) задач на доказательство. Задача решается «с двух сторон» — происходит анализ ситуации (с точки зрения цели; в данной задаче эта точка зрения заключается в том, что находятся не все совместные свойства чисел «abcabc», а те, что имеют отношение к дилимости) и анализ цели (релевантный данной задачи, с точки зрения ее условий). Этот анализ осуществляется в целом наугад, будучи ограниченным только упомянутыми «точками зрения». Наконец происходит «замыкание», когда анализ ситуации и анализ цели приводят к пониманию «решающего соотношение» (если общий делитель чисел делится на 13, то и сами числа делятся на 13). Важно, что решающее соотношение следует только когда какая-то его часть уже найдена более или менее случайными поисками. В данном случае части, о которых идет речь, следующие: число «abcabc» делятся на 1001; 1 001 делится на 13. Ни один из испытуемых в ходе решения не поставил вопрос, не имеют числа «abcabc» общего множителя, что делится на 13 (что соответствовало бы выявлению функционального значения решения в случае практических задач). Однако Дункера допускает, что это может происходить с опытными математиками.
Практические задачи
В качестве примеров можно привести несколько практических задач Дункера и функциональных значений их решений.
Экспериментальное исследование проблемной ситуации К.Дункером.



Мышление и инсайт [править]
Согласно определению Дункера, «мышление — это процесс, который посредством инсайта (понимания) проблемной ситуации приводит к адекватным ответным действиям». [1] Процесс, ведущий от стимула к ответному действию, Дункер называет инсайтным, если он непосредственно определяет содержание этого действия (в отличие от простого высвобождения стимулом уже готовой реакции). Это необходимо, когда такое действие не следует непосредственно из прошлого опыта.
Процесс решения задач [править]
Стадии решения задачи [править]
Согласно Дункеру, процесс решения задачи протекает следующим образом.
1. Сначала нужно понять проблемную ситуацию, то есть её внутренние связи; воспринять её как целое, заключающее в себе некий конфликт (например: обезьяна понимает, что её конечности слишком коротки, чтобы достать банан). «Понять что-либо означает приобрести гештальт или увидеть функциональное место его в гештальте». [4]
2. Из этого следует «функциональное значение» решения, которое, по словам Дункера, «находится на основе внутренних и очевидных связей с условиями проблемной ситуации» (например: необходим длинный предмет).
3. Потом функциональное значение решения конкретизируется, воплощается в определённое решение (например: палка). «Понять какое-либо решение как решение — это значит понять его как воплощение его функционального значения». [5]
Функциональное значение решения не является абстрактным, то есть общим для разных конкретных задач; «оно всецело возникает из данной проблемной ситуации», — пишет Дункер. Это доказывается тем, что при решении двух разных задач, имеющих общее функциональное значение решения, решение первой нисколько не помогает испытуемым при решении следующей за ней задачи, даже если они решают их подряд.
Процесс решения представляет собой развитие проблемы. Функциональное значение решения есть определенное преобразование первоначальной проблемы. И каждое новое свойство будущего решения, которое принимает в себя по ходу решения задачи функциональное значение, превращает функциональное значение в новую, более точно и определённо поставленную проблему. С каждым последующим преобразованием задачи процесс решения учитывает всё больше особенностей конкретной ситуации, постепенно проникая в её специфические условия и возможности. Дункер формулирует это так: «Конечная форма определённого решения в типическом случае достигается путём, ведущим через промежуточные фазы, из которых каждая обладает в отношении к предыдущим фазам характером решения, а в отношении к последующим — характером проблемы».
Анализ ситуации и цели [править]
На каждой фазе решения может быть поставлен вопрос о причинах конфликта («Почему я не могу достать банан руками?»), позволяющий глубже проникнуть в природу конфликта и приблизиться к решению («Потому что руки слишком коротки»). Дункер называет это «анализом конфликта».
Параллельно этому «углублению» может происходить и «горизонтальное» премещение между несколькими функциональными значениями, причём возвращаясь вновь к одному из функциональных значений, человек корректирует неудачный вариант решения, на котором остановился прежде, — по словам Дункера, ищет «в рамках прежней постановки вопроса другой зацепки для решения» или уточняет саму постановку вопроса.
Бывает, что не функциональное значение предшествует его конкретному воплощению, а, напротив, какой-то случайно бросившийся в глаза элемент ситуации (например, палка, замеченная обезьяной) наводит на мысль о его функциональном значении. Это может быть и результатом сознательного анализа «материала ситуации» («Что я могу использовать?»). Такой анализ ситуации особенно часто происходит при решении математических задач на доказательство.
Кроме описанного анализа ситуации (то есть анализа конфликта или материала) может происходить и анализ цели. Он выражается вопросами типа «Чего, собственно, я хочу?», «Без чего я могу обойтись?» и т. п. («Хочу ли я, чтобы банан оказался там, где сейчас я, или, может быть, я — там, где банан?»). Может происходить обобщение цели («Что вообще делают, когда хотят достать что-то на расстоянии?»). Анализ цели часто имеет место при решении математических задач на доказательство, когда преобразовывается то, что требуется доказать.
Задачи Дункера [править]
Дункер пользовался в своих экспериментах математическими и практическими задачами, предлагая испытуемым рассуждать вслух во время их решения.
Математические задачи [править]
Дункер обнаружил, что математические задачи решаются в основном при помощи анализа цели и анализа ситуации. Например, требуется объяснить, почему все числа вида «abcabc» (651 651, 274 274 и т. п.) делятся на 13. Вот один из протоколов эксперимента:
(1) Может быть, уже каждая тройка цифр делится на 13? (2) Может быть, здесь есть какое-либо правило суммирования цифр, как для случая делимости на 9? (3) Это должно следовать из какого-то скрытого общего принципа строения — первая тройка цифр в 10 раз больше второй, 591 591 есть 591 умноженное на 11, нет: умноженное на 101 (экспериментатор: «Верно?»), нет, на 1001. Не делится ли 1001 на 13?
Рассуждение (3), которое привело к решению, начинается с анализа цели: утверждение, что все числа вида «abcabc» делятся на 13, преобразуется в утверждение, что делимость на 13 следует из общих свойств чисел вида «abcabc». Затем начинается процесс анализа ситуации, направленный на поиск общих свойств чисел «abcabc», имеющих отношение к делимости. Это обычный путь решения математических (в том числе геометрических) задач на доказательство. Задача решается «с двух сторон» — происходит анализ ситуации (с точки зрения цели; в данной задаче эта точка зрения состоит в том, что отыскиваются не всякие общие свойства чисел «abcabc», а имеющие отношение к делимости) и анализ цели (релевантный данной задаче, с точки зрения её условий). Этот анализ осуществляется во многом наудачу, будучи ограниченным только упомянутыми «точками зрения». Наконец происходит «замыкание», когда анализ ситуации и анализ цели приводят к пониманию «решающего соотношения» (если общий делитель чисел делится на 13, то и сами числа делятся на 13).
Важно, что решающее соотношение всплывает только когда какая-то его конкретная часть уже обнаружена более или менее случайными поисками. В данном случае части, о которых идёт речь, таковы: числа «abcabc» делятся на 1001; 1001 делится на 13. Ни один из испытуемых не поставил в ходе решения вопрос о том, не имеют ли числа «abcabc» общего множителя, делящегося на 13 (что соответствовало бы обнаружению функционального значения решения в случае практических задач). Дункер, впрочем, допускает, что это может происходить с опытными математиками.
Практические задачи [править]
В качестве примеров можно привести несколько практических задач Дункера и функциональных значений их решений.
· Задача: «Предположим, что металлический шар падает на твёрдую металлическую поверхность. Известно, что после удара он подпрыгнет; этот факт обусловлен плоской деформацией шара при соприкосновении его с поверхностью. Упругие силы шара заставляют его принять прежнюю форму, что и вызывает его отталкивание (вспомните резиновый мяч). Вам нужно доказать наличие плоскостной деформации и найти способ, который мог бы не только показать наличие этого факта, но также форму и величину деформации».
Функциональное значение решения: «Функциональное значение наилучшего решения состоит в том, что находится третье, промежуточное, вещество, которым шар или поверхность окрашивается на месте предполагаемой деформации; оно наносится достаточно тонким слоем и легко оставляет след, что не изменяет условий задачи; кроме того, оно не обладает упругостью и поэтому сохраняет отпечаток круга».
· Задача. В другом эксперименте Дункер зачитывал испытуемым отрывок из «Гекльберри Финна» Марка Твена, в котором рассказывается, как Гекльберри Финн однажды переоделся в платье девочки; женщина, в доме которой он оказался, подозревает, что перед ней мальчик. Дункер предлагал испытуемым поставить себя на место этой женщины и придумать, как проверить свои подозрения.
«Функциональное значение решения заключается в следующем: поставить его [Гека] в типичные условия, при которых оба пола ведут себя по-разному; поставить его в необычные условия, когда предварительная подготовка окажется бесполезной или когда ситуация вызовет в нём мальчишеские привычки».
· Задача: «Надо найти прием для уничтожения неоперируемой опухоли желудка такими лучами, которые при достаточной интенсивности разрушают органические ткани, при этом окружающие опухоль здоровые части тела не должны быть разрушены».
Функциональные значения решений, предложенные Дункеру испытуемыми в ходе экспериментов:
1) устранить контакт между лучами и здоровыми тканями (одно из конкретных воплощений этого — послать лучи через пищевод);
2) понизить чувствительность здоровых тканей (например, с помощью инъекции);
3) понизить интенсивность лучей на пути через здоровые ткани (например, послать с разных сторон несколько слабых лучей, пересекающихся на опухоли). Последнее функциональное решение в указанном конкретном воплощении является наилучшим решением задачи; первые два неосуществимы на практике.
· Задача: «Представьте себе большой город, в одном из концов которого находится большая площадь. Однажды на площади произошло странное и очень занятное событие. Оно привлекло к себе тысячи людей и так как главная улица была самой широкой и удобной в городе и вела прямо на площадь, полицейским органам нужно было найти способ предотвращения блокады движения по главной улице, которая была загружена толпами людей. Какой способ предложили бы вы?».
Функциональные значения решений, предложенные Дункеру испытуемыми в ходе экспериментов:
1) устранить контакт между площадью и главной улицей;
2) поставить на улицах полицейских, которые будут контролировать поток людей, таким образом люди не смогут передвигаться всей толпой;
3) Остановить движение на главной улице, пустить людей по небольшим «окольным» улочкам. Таким образом люди смогут посмотреть событие и не создать блокаду главной улицы.
Тест Карла Данкера
Имеются: свеча, коробка спичек и коробка кнопок, требуется закрепить свечу на стене так, чтобы воск не капал на пол или на стену. Тест, как вы поняли, простой, но требует творческого подхода.
На рисунке — знаменитый тест, придуманный Карлом Данкером в 1935–ом году для экспериментов в области продуктивного мышления. Имеются: свеча, коробка спичек и коробка кнопок, требуется закрепить свечу на стене так, чтобы воск не капал на пол или на стену. Тест простой, решить задачу могут все, это лишь вопрос времени, либо творческого подхода.
Некоторые начинают с попытки прикрепить свечу к стене кнопками. Не получается. Другие … вижу-вижу, мне тут с места кто-то знаками показывает… Другие считают, что лучше всего зажечь свечу, расплавить кончик и приклеить её к стене. Идея грандиозная, но… не получается. В конечном итоге, минут эдак через 5-10, большинство участников находят решение: нужно высыпать кнопки из коробки, закрепить коробку на стене кнопками и поставить в неё свечу. Ключевой момент – преодоление т.н. функциональной фиксации: вы смотрите на коробку и видите лишь вместилище для кнопок. Но ведь она может иметь иную функцию, например, стать платформой для свечи. Вот она – «загадка свечи».
На основе этого теста ученый Сэм Глаксберг провёл эксперимент на тему силы стимулов. Набрав две группы добровольцев Глаксберг изложил им условия эксперимента так: «Я засекаю время, чтобы узнать, как быстро вы можете решить задачу?» Одной группе при этом он сказал: «Ваше время решения будет служить нормой, которая покажет сколько в среднем требуется типичному участнику для решения такой задачи». Второй группе он предложил вознаграждение, сказав: «Каждый, чье время будет среди лучших 25% результатов, получит 5 долларов. А самый лучший результат дня вознаграждается 20-ю долларами.»
Вопрос: Насколько быстрее вторая группа решила задачу? Ответ: В среднем, им понадобилось на три с половиной минуты больше. Повторюсь: больше, на 3,5 минуты. Но ведь так не должно быть! Я верю в свободный рынок и так он работать не должен, правда? Чтобы люди проявили себя лучше, их надо вознаграждать, разве нет? Премии, комиссионные, всё что угодно, дай им только стимул. Так работает бизнес. Но здесь что-то не срабатывает. Налицо стимул, рассчитанный на обострение мысли и ускорение творчества, но действует он прямо противоположно: притупляет мысль, мешает творчеству.
И что самое интересное: этот эксперимент – не какое-то там отклонение от норм, он повторялся много-много раз в течение почти 40 лет. Условные стимулы, «если сделаешь вот так, то получишь вот это», работают при определённых условиях, для многих видов работ, они либо не срабатывают, либо же, зачастую, просто вредят. Это открытие – одно из самых обоснованных в социальной науке. А также – одно из самых игнорируемых капитализмом.
Сэм Глаксберг проделал вариант того же эксперимента, в котором он преподнёс ту же задачку по-другому: кнопки были заранее извлечены из коробки. «Прикрепите свечу к стене, чтобы воск не капал на стол.» Те же условия. Одним: «мы вас замеряем для нормы», другим: «мы вам даем стимулы». Что же получилось на это раз? На этот раз мотивированная группа заткнула другую группу за пояс. Почему? Да потому, что, когда кнопки вне коробочки, задачка довольно легкая, не так ли?
Стимул «если…то….» очень хорошо воздействует в тех заданиях, где правила просты и направление работы очевидно. Награда, в силу своей природы, сужает наш фокус, концентрирует мозг, вот отчего она действенна во многих случаях. А потому, для такого рода заданий, когда узкое фокусирование на конкретной цели ведёт нас прямо к ней, вознаграждение срабатывает очень хорошо. Но решению настоящей «загадки свечи» такой взгляд не способствует. Решение не очевидно, оно за границей поля зрения. И нужно осмотреться вокруг, а не сужать наше поле зрения мотивацией на награду.
В последние несколько лет я заинтересовался наукой мотивации человека, в особенности динамикой внешних стимулов и стимулов внутренних. Скажу вам, что их воздействие весьма различно. Ситуация такова, что имеется разрыв между тем, что знает наука и тем, что практикует бизнес. Особенно тревожно то, что наша система функционирования бизнеса – имеется в виду набор предпосылок и соглашений, на которых зиждется бизнес, а именно, система мотивации и управления кадрами – вся она построена на основе именно внешних стимулов, на основе системы кнута и пряника. Вообще-то, это вполне нормально для типичной работы 20-го века. Но для типичной работы 21-го века, этот механистический подход кнута и пряника не подходит, часто не действует и часто противодействует.
В Западной Европе, во многих регионах Азии, в Северной Америке и в Австралии, «белые воротнички» всё меньше заняты механистическим видом работ, и всё больше – творческим видом работ. Установленные и отрегулированные виды работ левого полушария, часть работы по бухучёту и финансовому анализу, некоторые задачи программирования, стало довольно легко перепоручать в прочие страны, стало легко автоматизировать. Компьютер сделает вам это быстрее. Поставщики из стран с низкой оплатой труда сделают вам это дешевле. Намного важнее стали виды работ правого полушария, где заложены способности к творчеству и абстракции.
Однако имеется разрыв между тем, что известно науке и что практикуют компании. Я с беспокойством наблюдаю, посреди завала экономического кризиса, как огромное число организаций принимает решения по управлению своими ценными кадрами исходя из устаревших и непроверенных предпосылок, основанных более на «народной мудрости», чем на науке. А ведь для выхода из нынешних экономических неприятностей, для достижения высокой продуктивности в решении характерных для 21-го века задач, бежать быстрее в неправильном направлении – не решение. Привлекать пряником послаще – не решение, угрожать кнутом подлиннее – не решение. Нам срочно нужен абсолютно новый подход.
Сегодня я коснусь только самостоятельности. В 20-м веке появилась идея управления людьми, т.н. менеджмента. Так вот, менеджмент – не создание природы. Менеджмент – это как радиоприёмник, его изобрели. И никто не сказал, что он будет работать вечно. Менеджмент – это прекрасно, его традиционные идеи безупречны, если требуется исполнительность. Но когда нужно участие, намного лучший результат дает саморегуляция.
Я сейчас приведу пару примеров фундаментального толкования саморегуляции. В чем идея? Да, это нечасто встретишь, но налицо первые признаки рождения действительно захватывающих вещей. Идея в том, что во-первых, зарплата должна быть адекватной и справедливой, это без всяких сомнений. Этим вопрос денег снят с повестки дня. А затем работнику предоставляют большую долю самостоятельности. Обратимся к практике.
Приведу еще более радикальный пример той же идеи. Называется «Рабочие Условия Направленные Исключительно на Результат». Сокращенно: ROWE. Система разработана двумя американскими консультантами для примерно десяти компаний по всей Северной Америке. При ROWE, у работников нет графика выхода на работу. Они появляются на работе когда хотят. Нет определенного времени пребывания в офисе, можно вообще не приходить. Нужно только сделать работу. Как делать, когда делать, где делать – это каждый решает сам. Встречи и собрания в этих условиях – исключительно по желанию.
И каков результат? Практически повсеместно: рост продуктивности, рост участия работников в делах фирмы, рост удовлетворённости, падение текучести кадров. Самостоятельность, профессионализм, целенаправленность – на этих столпах надо строить новые условия продуктивной деятельности. Вы, наверно, скажете: «Ммм-да-с. Соблазнительно, но утопично.» Отвечу: «Нннет-с.» И предъявляю доказательства.
Середина 90-х, Microsoft начинает проект электронной энциклопедии Encarta. Были задействованы все нужные стимулы. Все правильные стимулы. Специалистам платили за написание и редактирование статей. Процессом руководили хорошо оплачиваемые менеджеры, соблюдая рамки бюджета и времени. А потом, через пару лет, появилась еще одна энциклопедия. На совсем другой модели, как мы знаем. Делай в своё удовольствие! Никакой оплаты – ни цента, ни евро, ни иены. Создавай! – потому, что тебе это нравится.
Давайте предположим, что каких-то 10 лет назад вы бы обратились к экономистам, в любой стране, и сказали: «У меня вопрос. Вот вам две разные модели создания энциклопедии. Если им придётся столкнуться лбами, чья возьмёт?» Так вот, 10 лет назад ни один серьёзный экономист, ни в одной стране мира, не мог бы предсказать победу модели Википедии.
Это была борьба титанов, борьба двух различных подходов. Это была битва века на арене мотивации, подобно поединку за звание чемпиона мира по боксу среди супер-тяжеловесов. На глазах у всех! Мотивация внутренняя выступает против внешней мотивации. Самостоятельность, профессионализм и целенаправленность против кнута и пряника. И кто победил? Внутренняя мотивация, самостоятельность, профессионализм и целенаправленность выбивают противника нокаутом. Я закругляюсь.
Имеется разрыв между научным знанием и деловой практикой. Что известно науке? Во-первых, типичные для 20-го века вознаграждения, те самые стимулы, которые считаются неотъемлемой частью умения вести бизнес, работают, но только в предельно узком диапазоне условий. Во-вторых, те же вознаграждения типа «если… то …» часто губят творчество. В-третьих, секрет высокой продуктивности не в системе награждения и наказания, а в невидимом внутреннем двигателе. Стремлении создавать вещи ради них самих. Стремлении делать что-то, потому что это важно.
Вот вам самое главное. Вот – самое лучшее. Честно говоря, мы это уже знали. Наука подтверждает то, что мы чуем сердцем. Так что, если нам удастся устранить разрыв между научным знанием и деловой практикой, если нам удастся утвердить наше понимание мотивации, и пронести его в 21-й век, если нам удастся отбросить ленивую по природе и опасную идеологию кнута и пряника, мы сможем усилить наш бизнес, мы сможем решить множество «загадок свечи» и возможно, возможно, возможно, нам удастся изменить мир.