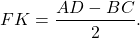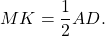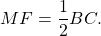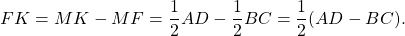докажите что отрезок соединяющий середины диагоналей трапеции равен полуразности оснований
Отрезок, соединяющий середины диагоналей трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Отрезок, соединяющий середины диагоналей трапеции
1) лежит на средней линии трапеции,
2) равен полуразности оснований трапеции.
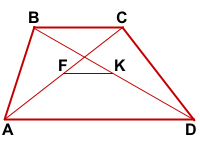
F — середина AC, K — середина BD,
MN — средняя линия трапеции
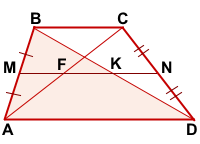
Рассмотрим угол ABD.
Так как AM=BM и MN||AD, то по теореме Фалеса, отрезки, на которые прямая MN делит BD, также равны, то есть MN пересекает отрезок BD в его середине, то есть в точке K.
Аналогично, для угла BAC:
AM=BM, MN||AD, следовательно, по теореме Фалеса прямая MN пересекает отрезок AC в его середине, то есть в точке F.
Таким образом, отрезок, соединяющий середины диагонали трапеции, параллелен основаниям трапеции и лежит на её средней линии.
MF — средняя линия треугольника ABC. Поэтому
Что и требовалось доказать.
Если использовать обозначения AD=a, BC=b, то формула длины отрезка, соединяющего середины диагоналей трапеции, примет вид