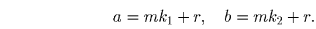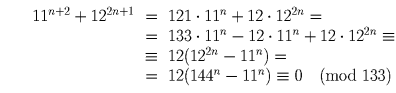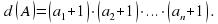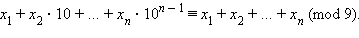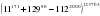докажите что 3099 61100 делится на 31
Докажите что 3099 61100 делится на 31
Задача 1:
Докажите, что a ≡ b (mod m) тогда и только тогда, когда a – b делится на m.
Решение:
Пусть a ≡ b (mod m). Обозначим одинаковый для a и b остаток при делении на m через r. Тогда
Отсюда a – b = m(k 1 – k 2 ) делится на m.
Задача 2:
Если a ≡ b (mod m) и c ≡ d (mod %)%m, то a + c ≡ b + d (mod %)%m.
Решение:
Так как a – b делится на m и c – d делится на m, то (a – b) + (c – d) = (a + c) – (b + d) делится на m, что и требовалось доказать.
Задача 3:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то a – c ≡ b – d (mod %)%m.
Задача 4:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то ac ≡ bd (mod %)%m.
Решение:
ac – bd = ac – bc + bc – bd = (a – b)c + b(c – d) делится на m, что и требовалось доказать.
Задача 5:
Если a ≡ b (mod %)%m, n – натуральное число, то a n ≡ b n (mod %)%m.
Задача 6:
Докажите, что n² + 1 не делится на 3 ни при каком целом n.
Решение:
Ясно, что каждое целое число n сравнимо по модулю 3 либо с 0, либо с 1, либо с 2.
Если n ≡ 0 (mod %)%3, то n² ≡ 0 (mod 3) – (умножение сравнений) и n² + 1 ≡ 1 (mod %)%3 – (сложение сравнений).
Если n ≡ 1 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Если n ≡ 2 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Таким образом, ни в одном случае мы не получим n² + 1 ≡ 0 (mod %)%3.
Задача 7:
Найдите остаток от деления 6¹ºº на 7.
Решение:
Заметим, что 6 ≡ – 1 (mod %)%7. Возводя это сравнение в сотую степень, получаем 6¹ºº ≡ ( – 1)¹ºº (mod %)%7, то есть 6¹ºº ≡ 1 (mod %)%7.
Задача 8:
Докажите, что 30 99 + 61¹ºº делится на 31.
Решение:
30 99 ≡ ( – 1) 99 ≡ – 1 (mod 31) 61¹ºº ≡ ( – 1)¹ºº ≡ 1 (mod 31).
Задача 9:
а) 43¹º¹ + 23¹º¹ делится на 66.
б) a n + b n делится на a + b, если n – нечетное число.
Решение:
б) a n + b n = (a + b)(a n – 1 – a n – 2 b + … + ( – 1) n – 1 b n – 1 )
Задача 10:
Докажите, что 1 n + 2 n + … + (n – 1) n делится на n при нечетном n.
Решение:
Указание: Рассмотрите сумму симметричных слагаемых.
Задача 11:
Докажите, что существует бесконечно много натуральных чисел, не представимых в виде суммы трех точных кубов.
Решение:
Рассмотрите числа вида 8k + 7.
Задача 12:
Докажите, что ни одно из чисел вида 10 3n + 1 нельзя представить в виде суммы двух кубов натуральных чисел.
Решение:
Куб натурального числа сравним по модулю 7 либо с 0, либо с 1, либо с – 1 – проверьте! Поэтому сумма двух кубов сравнима с одним из следующих чисел: – 2, – 1, 0, 1, 2. Заметим, что 10 ≡ 3 (mod %)%7, а 10³ ≡ – 1 (mod %)%7. Поэтому 10 3n + 1 сравнимо либо с 3, либо с – 3 по модулю 7.
Задача 13:
Докажите, что среди 51 целого числа найдутся два, квадраты которых дают одинаковые остатки при делении на 100.
Решение:
Используйте тождество x² – y² = (x – y)(x + y).
Задача 14:
Назовем натуральное число n удобным, если n² + 1 делится на 1000001. Докажите, что среди чисел 1, 2, …, 1000000 четное число удобных.
Решение:
Если x – удобное число, то и 1000001 – x – также удобное.
Задача 15:
а) Может ли квадрат натурального числа оканчиваться на 2?
б) Можно ли, используя только цифры 2, 3, 7, 8 (возможно, по несколько раз), составить квадрат натурального числа?
Решение:
Задача 16:
Какое число нужно добавить к числу (n² – 1)¹ººº (n² + 1)¹ºº¹, чтобы результат делился на n?
Решение:
Например, – 1 или n – 1.
Задача 17:
Найдите остаток от деления на 7 числа 10¹º + 10¹ºº + 10¹ººº + … + 10¹ºººººººººº.
Решение:
Задача 18:
Сколько существует натуральных чисел n, меньших 10000, для которых 2 n – n² делится на 7?
Решение:
Задача 19:
Обозначим через k произведение нескольких (больше одного) первых простых чисел. Докажите, что число а) k – 1; б) k + 1 не является точным квадратом.
Решение:
а) k – 1 = 3p + 2, а по модулю 3 квадраты могут давать лишь остатки 0 или 1.
б) k + 1 = 4q + 3, а по модулю 4 квадраты могут давать лишь остатки 0 или 1.
Задача 20:
Существует ли такое натуральное n, что n² + n + 1 делится на 1955?
Решение:
Нет. n² + n + 1 не может даже делиться на 5.
Задача 21:
Докажите, что 11 n + 2 + 12 2n + 1 делится на 133 при любом натуральном n.
Решение:
Задача 22:
Пусть n – натуральное число такое, что n + 1 делится на 24. Докажите, что сумма всех натуральных делителей n делится на 24.
Решение:
Докажите, что сумма делителей делится и на 3, и на 8.
Задача 23:
а) a 1 = a 2 = 1. Докажите, что ни один из членов последовательности не делится на 4.
б) Докажите, что a n – 22 – составное число при любом n > 10.
Решение:
Докажите что 3099 61100 делится на 31
Докажите, что
а) 2 41 + 1 делится на 83;
б) 2 70 + 3 70 делится на 13;
в) 2 60 – 1 делится на 20801.
Решение
а) 2 9 = 512 ≡ 14 (mod 83), 2 18 ≡ 196 ≡ 30, 2 36 ≡ 900 ≡ 70 ≡ –13, 2 41 ≡ –13·32 ≡ –416 ≡ –1.
б) 2 70 + 3 70 = 4 35 + 9 35 делится на 4 + 9 = 13.
в) 20801 = 11·31·61.
Первый способ. 2 60 – 1 делится на 2 10 – 1 = (2 5 – 1)(2 5 + 1) = 31·33. Это число делится на 31 и на 11. Кроме того, 2 6 ≡ 3 (mod 61), 2 30 ≡ 243 ≡ –1,
2 60 ≡ 1.
Второй способ. Согласно малой теореме Ферма (см. задачу 60736) 2 60 – 1 делится на 61, 2 30 – 1 делится на 31, 2 10 – 1 делится на 11. Поэтому
2 60 – 1 делится на все эти числа.
Замечания
В п. а) школьники, знакомые с квадратичными вычетами могут рассуждать так: (2 41 – 1)(2 41 + 1) = 2 82 – 1 делится на 83 по малой теореме Ферма. Двойка не является квадратичным вычетом по модулю 83, поэтому 2 41 – 1 на 83 не делится. Значит, на 83 делится 2 41 + 1.
Источники и прецеденты использования
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 4 |
| Название | Арифметика остатков |
| Тема | Деление с остатком. Арифметика остатков |
| параграф | |
| Номер | 2 |
| Название | Делимость |
| Тема | Теория чисел. Делимость (прочее) |
| задача | |
| Номер | 04.027 |
Статья по алгебре на тему «Теория вычетов: применения и перспективы»
Теория вычетов: применения и перспективы
Кабанова Галина Фёдоровна, учитель математики МБОУ «Костерёвская СОШ №2»
Петушинского района Владимирской области
Стремительно изменяется мир и сама жизнь. В нее входят новые технологии. Только математика и решение задач в традиционном понимании не изменяют себе. Математические законы проверены и систематизированы, поэтому человек в важные моменты может положиться на нее. Решить любую задачу. Математика не подведет. А умение правильно рассуждать, анализировать, подсчитывать в большей мере способствуют занятия математикой.
Теория чисел или высшая арифметика – самая древняя и самая интересная наука. Рождение математики – это появление натуральных чисел. Операции сложения и умножения возникли вместе с натуральными числами. Теория чисел связана с операцией деления. Целые числа отличаются от натуральных тем, что там есть операция вычитания и число ноль. Даже в самые далекие времена, когда люди жили в пещерах и одевались в звериные шкуры, они не могли обойтись без счета. Многие правила из школьных учебников математики были известны древним грекам две с лишним тысячи лет назад. Весомый вклад в становление теории чисел оказали пифагорцы, Евклид и Диофант. Теория делимости появилась в 399 году до нашей эры. Евклид посвятил ей книгу « VII Начал», в которой описал алгоритм нахождения наибольшего общего делителя двух чисел (алгоритм Евклида) и доказал бесконечность множества целых чисел. В 19 веке над теорией чисел работали многие видные ученые. Гауссом была создана теория сравнений, с помощью которой была создана теория сравнений, с помощью которой доказали ряд теорем о простых числах и изучены были свойства вычетов. Дальнейшим изучением распределения простых чисел занимал
123456 ≡ 1236 (mod 9),
2) Любое число сравнимо само с собой по любому модулю.
4) Сравнения можно складывать:
5) Сравнения можно перемножать:
6) Сравнения можно возводить в степень. Сокращать обе части сравнений нельзя, но если числа взаимно простые, то можно.
7) Если a ≡ b ( mod m ) и b ≡ c ( mod m ), то a ≡ c ( mod m ) (свойство транзитивности).
В теории чисел в первую очередь ставятся и решаются те проблемы, которые важны для математики и вычислительной науки в целом. В отдельный раздел теории чисел выделяются задачи на применение сравнений для решения задач на делимость. Пример одной из таких задач. Доказать, что 30 99 +61 100 делится на 31. Рассмотрим сравнения по модулю 31:
2 7 ≡ 2 ( mod 9) и так далее.
Так как 2005 ≡ 1 ( mod 6), то 2 2005 ≡ 2 ( mod 9), то есть ответом будет число 2.
Выполненные примеры основаны на свойствах сравнений и показывают, что вычеты являются мощным инструментом для решения нестандартных задач, позволяют доказывать делимость.
Понятие сравнения простое, оно не требует больших дополнительных знаний. Рассмотрим применение сравнений с отрицательными числами. Введем понятие двойного факториала. Двойной факториал – это произведение всех чисел одной четности с данным числом и не превосходящих это произведение.
Докажем, что сумма 1985!! И 1986!! Делится на 1987.
Основная идея этой задачи – это применение сравнений с отрицательными числами.
Сравнения можно перемножать. При умножении слева будет двойной факториал. Чисел слева будет 993.
1986!! ≡ (-1) 993 *1985!! ( mod 1987)
Разность этих чисел делится на 1987, значит, 1986!!+1985!! Делится на 1987, что и требовалось доказать. На примере решения этих задач убеждаемся в необходимости изучать понятие сравнений
1. Анерленд К. Роузен М. Классическое введение в современную теорию чисел. – М., 1987.
2. Бюро., Цагир Д. Рольфе Ю. Живые числа. – М., 1985.
3. Бухштаб А.А. Теория чисел – М.: «Просвещение», 1966.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Докажите что 3099 61100 делится на 31
Задача 85:
Пусть ka ≡ kb (mod %)%m, k и m – взаимно просты. Тогда a ≡ b (mod %)%m.
Решение:
Поскольку ka ≡ kb (mod %)%m, то ka – kb = k(a – b) делится на m. Так как k и m взаимно просты, то a – b делится на m, т.е. a ≡ b (mod %)%m.
Задача 86:
Пусть ka ≡ kb (mod kn). Тогда a ≡ b (mod %)%n.
Решение:
ka – kb делится на kn, т.е. k(a – b) = mkn. Следовательно, a – b = mn, ч.т.д.
Задача 87:
Найдите остаток от деления 2¹ºº на 101.
Решение:
Вследствие малой теоремы Ферма, он равен 1.
Задача 88:
Найдите остаток от деления 3¹º² на 101.
Решение:
Так как 101 – простое число, то 3¹ºº ≡ 1 (mod 101). Отсюда 3¹º² ≡ 9 3¹ºº = 9 (mod 101).
Задача 89:
Докажите, что 300³ººº – 1 делится на 1001.
Решение:
300³ººº = (300 500 ) 6 ≡ 1 (mod 7). Аналогично, 300³ººº ≡ 1 (mod 11) и (mod 13). Следовательно, 300³ººº – 1 делится и на 7, и на 11, и на 13, т.е. на 1001.
Задача 90:
Найдите остаток от деления 8 900 на 29.
Решение:
Задача 91:
Докажите, что 7¹²º – 1 делится на 143.
Решение:
Докажем, что 7¹²º – 1 делится на 11 и на 13. Действительно, (7¹²)¹º ≡ 1 (mod 11) и (7¹º)¹² ≡ 1 (mod 13).
Задача 92:
Докажите, что число 30 239 + 239³º – составное.
Решение:
Это число делится на 31.
Задача 93:
Пусть p – простое число. Докажите, что (a + b) p = a p + b p (mod %)%p для любых целых a и b.
Решение:
(a + b) p ≡ (a + b) = a + b ≡ a p + b p (mod p).
Задача 94:
Сумма трех чисел a, b и c делится на 30. Докажите, что a 5 + b 5 + c 5 также делится на 30.
Решение:
Докажите, что для произвольного целого x верно сравнение x 5 ≡ x (mod 30).
Задача 95:
Пусть p и q – различные простые числа. Докажите, что
а) p q + q p = p + q (mod pq).
б) 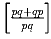
Решение:
Докажите, что p q + q p – p – q делится и на p, и на q.
Задача 96:
Пусть p – простое число, и a не делится на p. Докажите, что найдется натуральное число b, для которого ab ≡ 1 (mod p).
Решение:
Задача 97:
(Теорема Вильсона). Пусть p – простое число. Докажите, что (p – 1)! ≡ – 1 (mod %)%p.
Задача 98:
Пусть n – натуральное число, не кратное 17. Докажите, что либо n 8 + 1, либо n 8 – 1 делится на 17.
Решение:
(n 8 + 1)(n 8 – 1) = n 16 – 1 = 0 (mod 17).
Задача 99:
а) Пусть p – простое число, отличное от 3. Докажите, что число 111 … 11 (p единиц) не делится на p.
б) Пусть p > 5 – простое число. Докажите, что число 111 … 11 (p – 1 единица) делится на p.
Решение:
а) 111 … 11 (p единиц) = (10 p – 1)/9, а 10 p – 1 не делится на p, так как 10 p – 1 ≡ 10 – 1 = 9 (mod p).
б) 111 … 11 (p – 1 единица) = (10 p – 1 – 1)/9, а 10 p – 1 – 1 делится на p, так как p взаимно просто с 10 и с 9.
Задача 100:
Докажите, что для любого простого p разность 111 … 11222 … 22333 … 33 … 888 … 88999 … 99 – 123456789 (в первом числе каждая ненулевая цифра написана p раз) делится на p.
Решение:
Воспользуйтесь тем, что 10 p ≡ 10 (mod p), 10 2p ≡ 100 (mod p), …, 10 8p ≡ 10 8 (mod p).
Делимость. Деление с остатком. Сравнение по модулю. Задачи олимпиад.
Простые и составные числа.
Основная теорема арифметики.
НОД. НОК. Алгоритм Евклида.
Деление с остатком.
Задачи олимпиад.
Нажмите на картинку, чтобы посмотреть видео этого занятия
Конспект занятия «Делимость. Деление с остатком. Сравнение по модулю. Задачи олимпиад.»
Файл к уроку 8-9 класс
Делимость. Основная теорема арифметики. Деление с остатком. Сравнение по модулю.
Сегодня на занятии мы поговорим о натуральных числах, вспомним, что такое простые и составные числа, делители числа, и поработаем с основной теоремой арифметики.
Говорят, что число а делится на b (или говорят, что число b делитель числа a ), если существует число с такое, что а= bc .
Простые числа – числа, имеющие ровно 2 делителя.
Составные числа – числа, имеющие больше двух делителей.
Взаимно простые числа – числа, не имеющие общих простых делителей, то есть НОД их равен 1.
Основная теорема арифметики: любое натуральное число единственным образом представимо в виде произведения степеней простых чисел 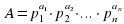
Если число 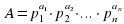
Пример: Найдите количество натуральных делителей числа 84.
Разложим 84 на простые множители:
Таким образом, каноническое разложение имеет вид 84=2 2 ·3·7. Тогда число натуральных делителей равно (2+1)·(1+1)·(1+1)=12.
Существует ли натуральное число, произведение цифр которого равно 1365?
Сколько существует целых чисел от 1 до 16500, которые
б) не делятся ни на 5, ни на 3;
в) не делятся ни на 5, ни на 3, ни на 11?
Ваня задумал простое трёхзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух?
Найдите все простые числа p и q, для которых выполняется равенство p 2 – 2q 2 = 1.
Найдите все натуральные n 1, для которых n 3 – 3 делится на n – 1.
Сумма двух целых чисел равна 101, а разность их квадратов – простое число. Найдите эти числа.
Произведение двух натуральных чисел, каждое из которых не делится нацело на 10, равно 1000. Найдите их сумму.
Тема: Деление с остатком.
Если от некоторого трехзначного числа отнять 6, то оно разделится на 7, если отнять 7, то оно разделится на 8, а если отнять 8, то оно разделится на 9. Определите это число.
Докажите, что если a и 5a имеют одинаковую сумму цифр, то a делится на 9.
Работа с остатками важна не только для вычисления неких недостающих чисел, но и для доказательства утверждений о делимости. Рассмотрим следующие примеры:
Доказать, что если р и р 2 +2 – простые числа, то и р 3 +4 – тоже простое.
Докажите, что а 2 — а четно при любом целом а.
Задача 11 является частным случаем этой теоремы (р=2);
Сформулируем и докажем теорему для р=3 и р=5.
Докажите, что если a нечётно, то a 2 – 1 делится на 8.
Докажите, что при любом целом n число n (2 n + 1)(7 n + 1) делится на 6.
Докажите, что каковы бы ни были целые числа a , b , с, число a 2 + b 2 + с 2 + 1 не делится на 8.
Докажите, что если a и b – нечётные числа, то a 2 — b 2 делится на 8.
Когда речь заходит об остатках, можно применять сравнение по модулю.
Два натуральных числа a и b, разность которых кратна натуральному числу m, называются сравнимыми по модулю m:
Пусть ab ≡ 0 (mod m), и числа a и m взаимно просты. Тогда b ≡ 0 (mod m).
Пример: Доказать свойство делимости на 9: число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.
Произвольное число 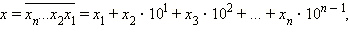
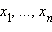
Пример: Свойство делимости на 19. Доказать, что число делится без остатка на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19.
Для любого натурального x верно равенство x = x1 + 10x2, где x1 – число единиц, x2 – число десятков этого числа. Пусть y = x2 + 2x1(то есть y – число десятков, сложенное с удвоенным числом единиц). Тогда 10y – x = 19x1 ≡ 0 (mod 19), откуда следует, что x ≡ 0 (mod 19) тогда и только тогда, когда 10y ≡ 0 (mod 19), то есть y ≡ 0 (mod 19). Утверждение доказано.
Доказать, что число 30 99 +61 100 делится на 31.
У числа 2 2016 находят сумму цифр, у нового числа также находят сумму его цифр, и так до тех пор, пока число не станет однозначным. Какое число получат в конце?
Сравнение по модулю.
Найдите остаток от деления на 5 числа