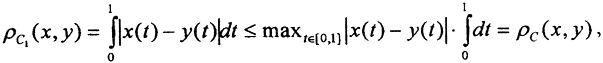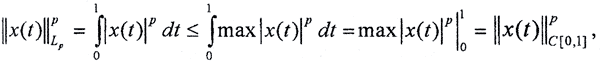доказать что метрики эквивалентны
Доказать что метрики эквивалентны
1.4.5. Сравнение метрик (норм)
Пусть на носителе метрического пространства X заданы две метрики ρ1 и ρ2.
Определение 1. Метрика (норма) ρ1 сильнее, чем метрика (норма) ρ2, если из сходимости последовательности
Определение 2. Две метрики (нормы) ρ1 и ρ2 эквивалентны, если из сходимости последовательности
Теорема 1. В любых конечномерных пространствах все метрики (нормы) эквивалентны.
Рассмотрим нормированное пространство (X,||x||), dim(X,||x||) = n, система векторов 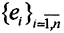
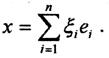
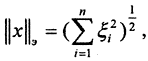
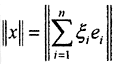
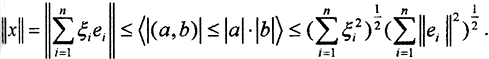
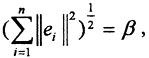
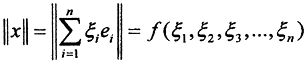
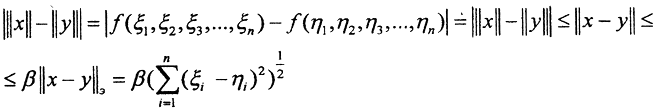
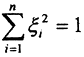
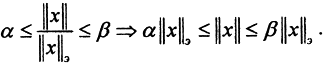
Пример. Доказать, что метрика ρС пространства С[0,1] сильнее метрики ρC1 пространства C1[0,1].
( Комментарий. В конечномерных пространствах все метрики (нормы) топологически эквивалентны в следующем смысле: для шара B(х0,R) радиусом R с центром в точке x0, построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.)
Пример. Покажем, что чебышевская норма, по крайней мере, не слабее гёльдеровской, а дифференциальная не слабее чебышёвской.
но 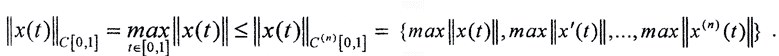
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Эквивалентные метрики
Надо показать, что метрики 

Включение 
| Заслуженный участник |
| Заслуженный участник |
Чем шары в первой метрике отличаются от шаров во второй.
Последний раз редактировалось Бабай 11.12.2011, 20:26, всего редактировалось 4 раз(а).
То что 


Так, ну шары с центром в фиксированной точке 







Напишу, для полноты, то, что я поначалу намалевал.
Нам надо найти 












| Заслуженный участник |
Из только строгой монотонности это не следует.
Последний раз редактировалось Бабай 11.12.2011, 21:36, всего редактировалось 1 раз.
А чего же Вам не хватает?
| Заслуженный участник |
Последний раз редактировалось arseniiv 11.12.2011, 22:48, всего редактировалось 5 раз(а).
Если не ошибаюсь во всём следующем; чтобы шар в первой метрике был шаром во второй, нужно, чтобы 







P. S. Нет, не всё. Надо показать, что сужение 
P. P. S. Очевидно, 



| Заслуженный участник |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
СОДЕРЖАНИЕ
Определение
Метрика называется ультраметрикой, если она удовлетворяет следующей более сильной версии неравенства треугольника, когда точки никогда не могут попадать «между» другими точками:
Метрика d на группе G (записанная мультипликативно) называется левоинвариантной (соответственно правоинвариантной ), если мы имеем
Примечания
Примеры
Эквивалентность показателей
Для данного множества X две метрики d 1 и d 2 называются топологически эквивалентными ( равномерно эквивалентными ), если тождественное отображение
Метрика, индуцированная нормой
Нормы на векторных пространствах эквивалентны определенным метрикам, а именно однородным, трансляционно-инвариантным. Другими словами, каждая норма определяет метрику, а некоторые метрики определяют норму.
Точно так же полунорма индуцирует псевдометрику (см. Ниже), а однородная псевдометрика, инвариантная относительно сдвигов, индуцирует полунорму.
Метрики на мультимножествах
Обобщенные метрики
Расширенные метрики
Псевдометрика
Квазиметрики
Иногда квазиметрика определяется как функция, удовлетворяющая всем аксиомам метрики, за исключением, возможно, симметрии. Название этого обобщения не совсем стандартизировано.
Квазиметрику вещественных чисел можно определить, задав
Метаметрики
В метаметрике выполняются все аксиомы метрики, за исключением того, что расстояние между идентичными точками не обязательно равно нулю. Другими словами, аксиомы метаметрики:
Полиметрика
Некоторые авторы работают с более слабой формой неравенства треугольника, например:
Преметрики
Это нестандартный термин. Иногда он используется для обозначения других обобщений показателей, таких как псевдосемиметрика или псевдометрика; в переводах русских книг иногда встречается как «праметрический». Преметрика, удовлетворяющая симметрии, то есть псевдосемиметрика, также называется расстоянием.
Это определяет преметрику на множестве степеней преметрического пространства. Если мы начнем с (псевдополеметрического) пространства, мы получим псевдосемиметрику, то есть симметричную преметрику. Любая преметрика приводит к следующему оператору предварительного закрытия cl :
Псевдоквазиметрия
Расстояние Лукашика-Кармовского
Важные случаи обобщенных показателей
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Эквивалентность топологий, порождаемых разными метриками
Последний раз редактировалось PAV 08.04.2012, 15:21, всего редактировалось 3 раз(а).
| Заслуженный участник |
Никак, не метриками, а нормами
Никак, не метриками, а нормами
Последний раз редактировалось MaximVD 24.12.2011, 19:34, всего редактировалось 1 раз.
Никак, не метриками, а нормами
Неужели метрика
порождает туже самую топологию, что и евклидова?
Последний раз редактировалось Oleg Zubelevich 24.12.2011, 19:50, всего редактировалось 2 раз(а).
Последний раз редактировалось Oleg Zubelevich 24.12.2011, 20:16, всего редактировалось 5 раз(а).
Последний раз редактировалось TILL 24.12.2011, 20:10, всего редактировалось 1 раз.
Последний раз редактировалось Oleg Zubelevich 24.12.2011, 20:24, всего редактировалось 2 раз(а).
Последний раз редактировалось TILL 24.12.2011, 20:27, всего редактировалось 1 раз.
Последний раз редактировалось lim 21.03.2016, 11:04, всего редактировалось 1 раз.
| Заслуженный участник |
Последний раз редактировалось alcoholist 21.03.2016, 11:02, всего редактировалось 4 раз(а).
Другую. Тоже согласованную с линейной структурой.
На евклидовой свет клином не сошелся.
В силу симметричности метрики 

Следовательно, любые две взятые с потолка метрики 

Это, конечно, верно в конечномерном пространстве. Но и только. В бесконечномерном случае это уже не так.

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей